Group conditional validity via multi-group learning

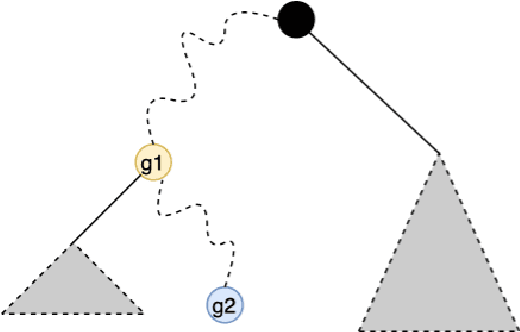
We consider the problem of distribution-free conformal prediction and the criterion of group conditional validity. This criterion is motivated by many practical scenarios including hidden stratification and group fairness. Existing methods achieve such guarantees under either restrictive grouping structure or distributional assumptions, or they are overly-conservative under heteroskedastic noise. We propose a simple reduction to the problem of achieving validity guarantees for individual populations by leveraging algorithms for a problem called multi-group learning. This allows us to port theoretical guarantees from multi-group learning to obtain obtain sample complexity guarantees for conformal prediction. We also provide a new algorithm for multi-group learning for groups with hierarchical structure. Using this algorithm in our reduction leads to improved sample complexity guarantees with a simpler predictor structure.

Intrinsic dimensionality and generalization properties of the $\mathcal{R}$-norm inductive bias

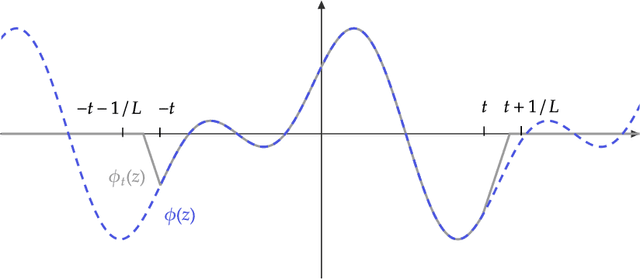
We study the structural and statistical properties of $\mathcal{R}$-norm minimizing interpolants of datasets labeled by specific target functions. The $\mathcal{R}$-norm is the basis of an inductive bias for two-layer neural networks, recently introduced to capture the functional effect of controlling the size of network weights, independently of the network width. We find that these interpolants are intrinsically multivariate functions, even when there are ridge functions that fit the data, and also that the $\mathcal{R}$-norm inductive bias is not sufficient for achieving statistically optimal generalization for certain learning problems. Altogether, these results shed new light on an inductive bias that is connected to practical neural network training.

Support vector machines and linear regression coincide with very high-dimensional features

The support vector machine (SVM) and minimum Euclidean norm least squares regression are two fundamentally different approaches to fitting linear models, but they have recently been connected in models for very high-dimensional data through a phenomenon of support vector proliferation, where every training example used to fit an SVM becomes a support vector. In this paper, we explore the generality of this phenomenon and make the following contributions. First, we prove a super-linear lower bound on the dimension (in terms of sample size) required for support vector proliferation in independent feature models, matching the upper bounds from previous works. We further identify a sharp phase transition in Gaussian feature models, bound the width of this transition, and give experimental support for its universality. Finally, we hypothesize that this phase transition occurs only in much higher-dimensional settings in the $\ell_1$ variant of the SVM, and we present a new geometric characterization of the problem that may elucidate this phenomenon for the general $\ell_p$ case.