Signaling and Social Learning in Swarms of Robots

This paper investigates the role of communication in improving coordination within robot swarms, focusing on a paradigm where learning and execution occur simultaneously in a decentralized manner. We highlight the role communication can play in addressing the credit assignment problem (individual contribution to the overall performance), and how it can be influenced by it. We propose a taxonomy of existing and future works on communication, focusing on information selection and physical abstraction as principal axes for classification: from low-level lossless compression with raw signal extraction and processing to high-level lossy compression with structured communication models. The paper reviews current research from evolutionary robotics, multi-agent (deep) reinforcement learning, language models, and biophysics models to outline the challenges and opportunities of communication in a collective of robots that continuously learn from one another through local message exchanges, illustrating a form of social learning.

Hearing the shape of an arena with spectral swarm robotics

Swarm robotics promises adaptability to unknown situations and robustness against failures. However, it still struggles with global tasks that require understanding the broader context in which the robots operate, such as identifying the shape of the arena in which the robots are embedded. Biological swarms, such as shoals of fish, flocks of birds, and colonies of insects, routinely solve global geometrical problems through the diffusion of local cues. This paradigm can be explicitly described by mathematical models that could be directly computed and exploited by a robotic swarm. Diffusion over a domain is mathematically encapsulated by the Laplacian, a linear operator that measures the local curvature of a function. Crucially the geometry of a domain can generally be reconstructed from the eigenspectrum of its Laplacian. Here we introduce spectral swarm robotics where robots diffuse information to their neighbors to emulate the Laplacian operator - enabling them to "hear" the spectrum of their arena. We reveal a universal scaling that links the optimal number of robots (a global parameter) with their optimal radius of interaction (a local parameter). We validate experimentally spectral swarm robotics under challenging conditions with the one-shot classification of arena shapes using a sparse swarm of Kilobots. Spectral methods can assist with challenging tasks where robots need to build an emergent consensus on their environment, such as adaptation to unknown terrains, division of labor, or quorum sensing. Spectral methods may extend beyond robotics to analyze and coordinate swarms of agents of various natures, such as traffic or crowds, and to better understand the long-range dynamics of natural systems emerging from short-range interactions.

Exploring Self-Assembling Behaviors in a Swarm of Bio-micro-robots using Surrogate-Assisted MAP-Elites

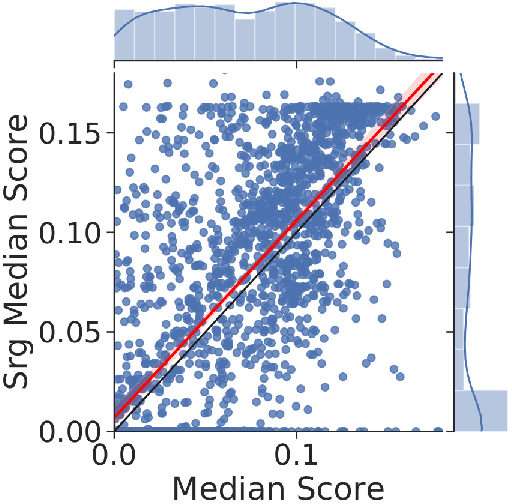
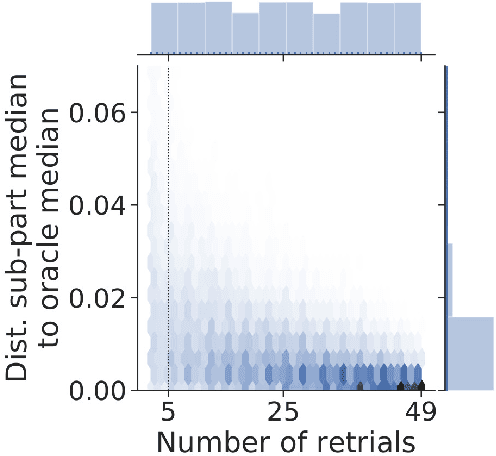
Swarms of molecular robots are a promising approach to create specific shapes at the microscopic scale through self-assembly. However, controlling their behavior is a challenging problem as it involves complex non-linear dynamics and high experimental variability. Hand-crafting a molecular controller will often be time-consuming and give sub-optimal results. Optimization methods, like the bioNEAT algorithm, were previously employed to partially overcome these difficulties, but they still had to cope with deceptive high-dimensional search spaces and computationally expensive simulations. Here, we describe a novel approach to solve this problem by using MAP-Elites, an algorithm that searches for both high-performing and diverse solutions. We then apply it to a molecular robotic framework we recently introduced that allows sensing, signaling and self-assembly at the micro-scale and show that MAP-Elites outperforms previous approaches. Additionally, we propose a surrogate model of micro-robots physics and chemical reaction dynamics to reduce the computational costs of simulation. We show that the resulting methodology is capable of optimizing controllers with similar accuracy as when using only a full-fledged realistic model, with half the computational budget.