Natalie Doss
Optimal estimation of high-dimensional Gaussian mixtures
Feb 14, 2020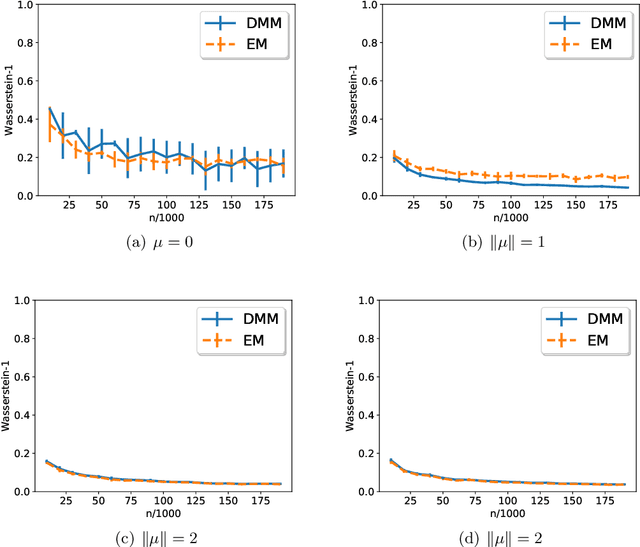
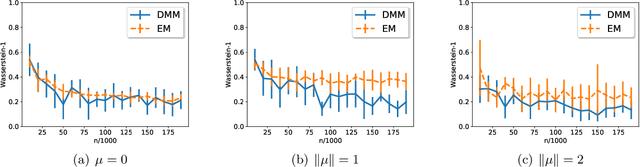
Abstract:This paper studies the optimal rate of estimation in a finite Gaussian location mixture model in high dimensions without separation conditions. We assume that the number of components $k$ is bounded and that the centers lie in a ball of bounded radius, while allowing the dimension $d$ to be as large as the sample size $n$. Extending the one-dimensional result of Heinrich and Kahn \cite{HK2015}, we show that the minimax rate of estimating the mixing distribution in Wasserstein distance is $\Theta((d/n)^{1/4} + n^{-1/(4k-2)})$, achieved by an estimator computable in time $O(nd^2+n^{5/4})$. Furthermore, we show that the mixture density can be estimated at the optimal parametric rate $\Theta(\sqrt{d/n})$ in Hellinger distance; however, no computationally efficient algorithm is known to achieve the optimal rate. Both the theoretical and methodological development rely on a careful application of the method of moments. Central to our results is the observation that the information geometry of finite Gaussian mixtures is characterized by the moment tensors of the mixing distribution, whose low-rank structure can be exploited to obtain a sharp local entropy bound.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge