Narges Mohammadi
Combining physics-based modeling and deep learning for ultrasound elastography
Jul 28, 2021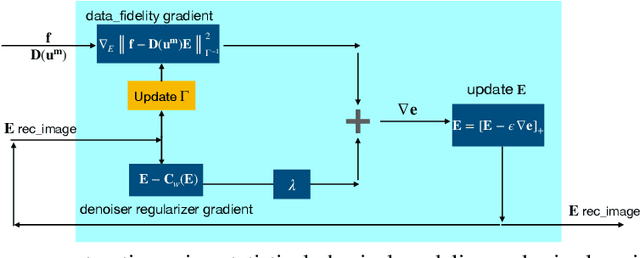

Abstract:Ultrasound elasticity images which enable the visualization of quantitative maps of tissue stiffness can be reconstructed by solving an inverse problem. Classical model-based approaches for ultrasound elastography use deterministic finite element methods (FEMs) to incorporate the governing physical laws resulting in poor performance in noisy conditions. Moreover, these approaches utilize fixed regularizers for various tissue patterns while appropriate data-adaptive priors might be required for capturing the complex spatial elasticity distribution. In this regard, we propose a joint model-based and learning-based framework for estimating the elasticity distribution by solving a regularized optimization problem. We present an integrated objective function composed of a statistical physics-based forward model and a data-driven regularizer to leverage deep neural networks for learning the underlying elasticity prior. This constrained optimization problem is solved using the gradient descent (GD) method and the gradient of regularizer is simply replaced by the residual of the trained denoiser network for having an explicit objective function with reduced computation time.
Regularization by Adversarial Learning for Ultrasound Elasticity Imaging
Jun 14, 2021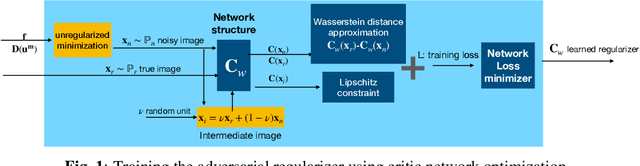
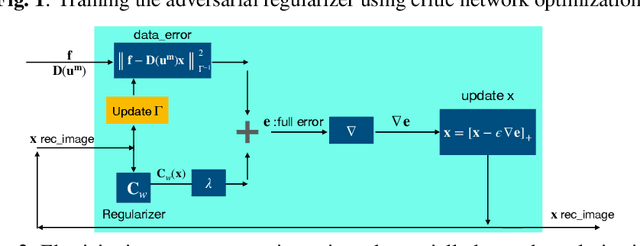
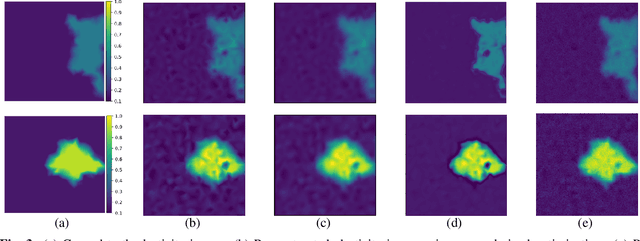
Abstract:Classical model-based imaging methods for ultrasound elasticity inverse problem require prior constraints about the underlying elasticity patterns, while finding the appropriate hand-crafted prior for each tissue type is a challenge. In contrast, standard data-driven methods count solely on supervised learning on the training data pairs leading to massive network parameters for unnecessary physical model relearning which might not be consistent with the governing physical models of the imaging system. Fusing the physical forward model and noise statistics with data-adaptive priors leads to a united reconstruction framework that guarantees the learned reconstruction agrees with the physical models while coping with the limited training data. In this paper, we propose a new methodology for estimating the elasticity image by solving a regularized optimization problem which benefits from the physics-based modeling via a data-fidelity term and adversarially learned priors via a regularization term. In this method, the regularizer is trained based on the Wasserstein Generative Adversarial Network (WGAN) objective function which tries to distinguish the distribution of clean and noisy images. Leveraging such an adversarial regularizer for parameterizing the distribution of latent images and using gradient descent (GD) for solving the corresponding regularized optimization task leads to stability and convergence of the reconstruction compared to pixel-wise supervised learning schemes. Our simulation results verify the effectiveness and robustness of the proposed methodology with limited training datasets.
MR elasticity reconstruction using statistical physical modeling and explicit data-driven denoising regularizer
May 27, 2021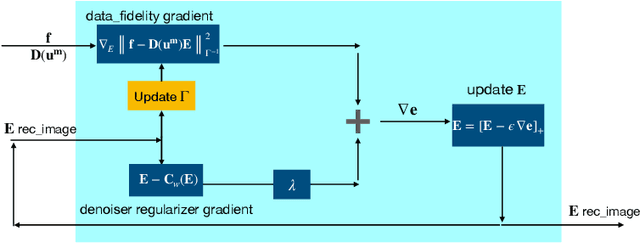
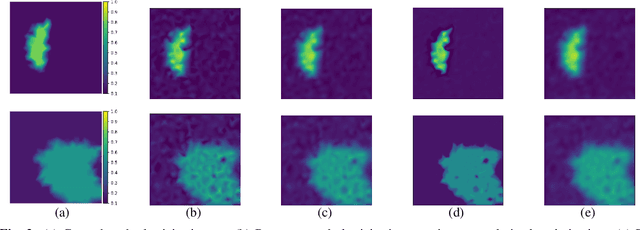
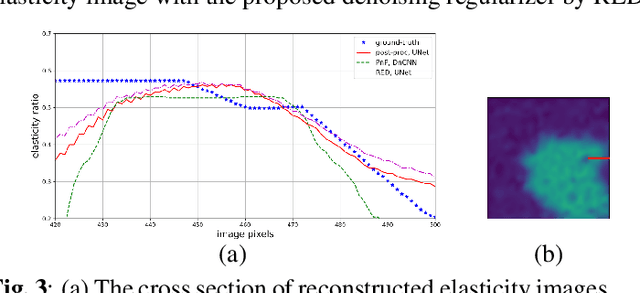
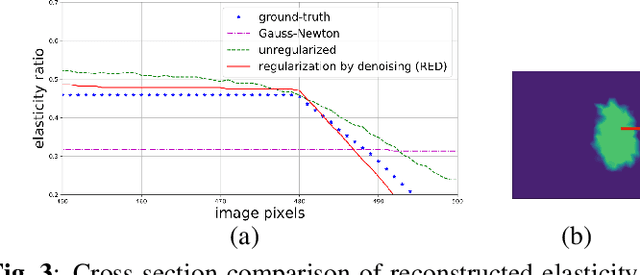
Abstract:Elasticity image, visualizing the quantitative map of tissue stiffness, can be reconstructed by solving an inverse problem. Classical methods for magnetic resonance elastography (MRE) try to solve a regularized optimization problem comprising a deterministic physical model and a prior constraint as data-fidelity term and regularization term, respectively. For improving the elasticity reconstructions, appropriate prior about the underlying elasticity distribution is required which is not unique. This article proposes an infused approach for MRE reconstruction by integrating the statistical representation of the physical laws of harmonic motions and learning-based prior. For data-fidelity term, we use a statistical linear-algebraic model of equilibrium equations and for the regularizer, data-driven regularization by denoising (RED) is utilized. In the proposed optimization paradigm, the regularizer gradient is simply replaced by the residual of learned denoiser leading to time-efficient computation and convex explicit objective function. Simulation results of elasticity reconstruction verify the effectiveness of the proposed approach.
Finite Element Reconstruction Of Stiffness Images In MR Elastography Using Statistical Physical Forward Modeling And Proximal Optimization Methods
Mar 26, 2021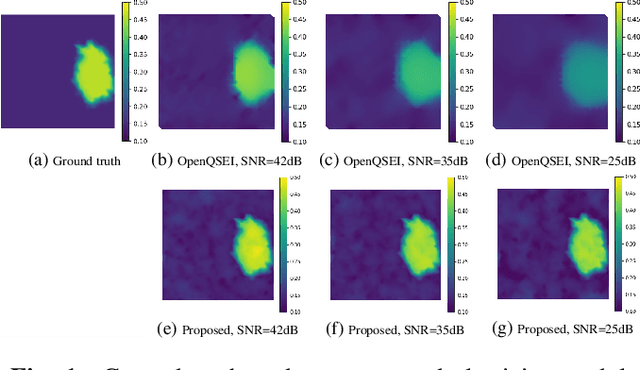
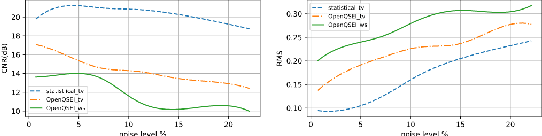
Abstract:Quantitative characterization of tissue properties, known as elasticity imaging, can be cast as solving an ill-posed inverse problem. The finite element methods (FEMs) in magnetic resonance elastography (MRE) imaging are based on solving a constrained optimization problem consisting of a physical forward model and a regularizer as the data-fidelity term and the prior term, respectively. In existing formulation for the elasticity forward model, physical laws that arise from equilibrium equation of harmonic motion, indicate a deterministic relationship between MRE-measured data and unknown elasticity distribution which leads to the poor and unstable elasticity distribution estimation in the presence of noise. Toward this end, we propose an efficient statistical methodology for physical forward model refinement by formulating it as linear algebraic representation with respect to the unknown elasticity distribution and incorporating an analytical noise model. To solve the subsequent total variation regularized optimization task, we benefit from a fixed-point scheme involving proximal gradient methods. Simulation results of elasticity reconstruction in various SNR conditions verify the effectiveness of the proposed approach.
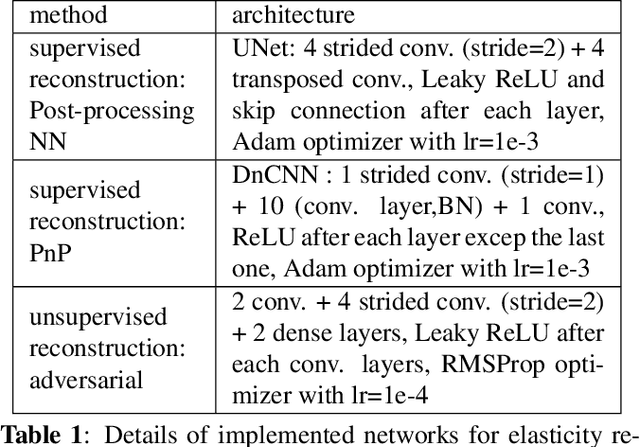
Ultrasound Elasticity Imaging Using Physics-based Models And Learning-based Plug-And-Play Priors
Mar 25, 2021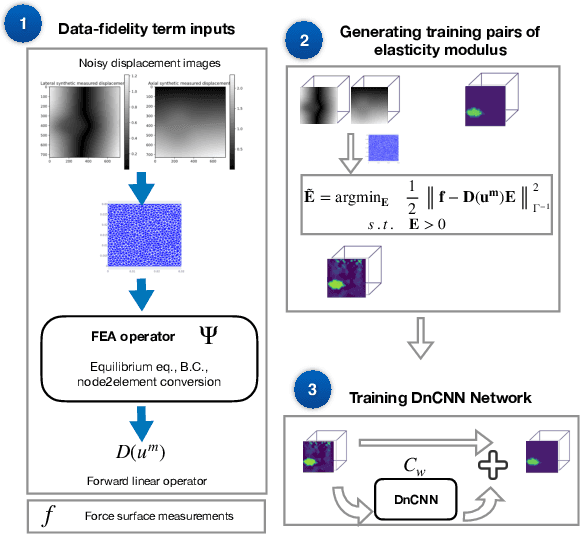
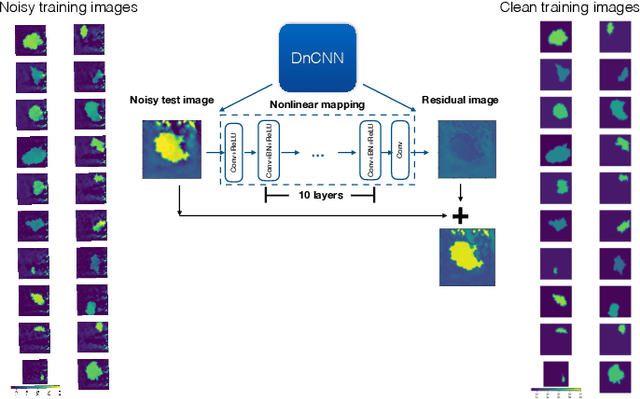
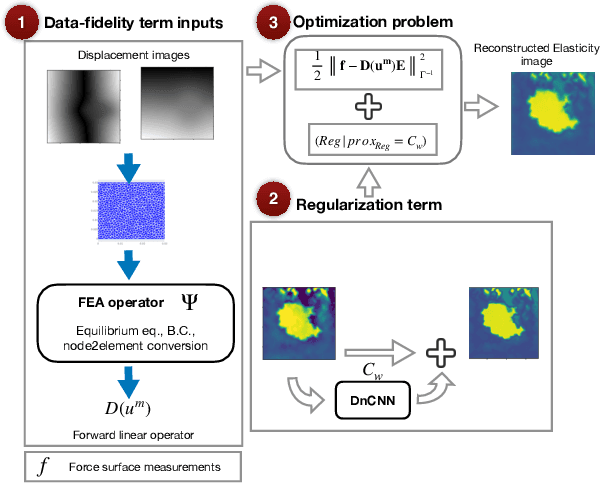
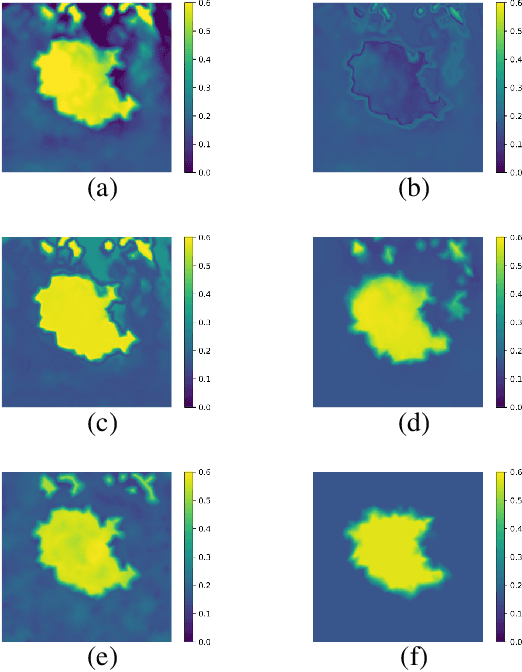
Abstract:Existing physical model-based imaging methods for ultrasound elasticity reconstruction utilize fixed variational regularizers that may not be appropriate for the application of interest or may not capture complex spatial prior information about the underlying tissues. On the other hand, end-to-end learning-based methods count solely on the training data, not taking advantage of the governing physical laws of the imaging system. Integrating learning-based priors with physical forward models for ultrasound elasticity imaging, we present a joint reconstruction framework which guarantees that learning driven reconstructions are consistent with the underlying physics. For solving the elasticity inverse problem as a regularized optimization problem, we propose a plug-and-play (PnP) reconstruction approach in which each iteration of the elasticity image estimation process involves separate updates incorporating data fidelity and learning-based regularization. In this methodology, the data fidelity term is developed using a statistical linear algebraic model of quasi-static equilibrium equation revealing the relationship of the observed displacement fields \cmmnt{measured deformation data} to the unobserved elastic modulus. The regularizer comprises a convolutional neural network (CNN) based denoiser that captures the learned prior structure of the underlying tissues. Preliminary simulation results demonstrate the robustness and effectiveness of the proposed approach with limited training datasets and noisy displacement measurements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge