Finite Element Reconstruction Of Stiffness Images In MR Elastography Using Statistical Physical Forward Modeling And Proximal Optimization Methods
Paper and Code
Mar 26, 2021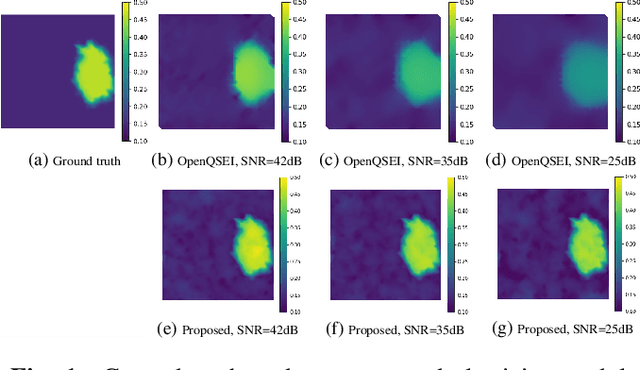
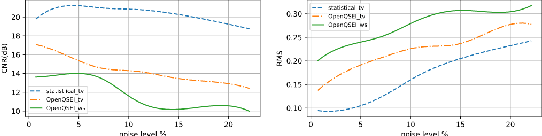
Quantitative characterization of tissue properties, known as elasticity imaging, can be cast as solving an ill-posed inverse problem. The finite element methods (FEMs) in magnetic resonance elastography (MRE) imaging are based on solving a constrained optimization problem consisting of a physical forward model and a regularizer as the data-fidelity term and the prior term, respectively. In existing formulation for the elasticity forward model, physical laws that arise from equilibrium equation of harmonic motion, indicate a deterministic relationship between MRE-measured data and unknown elasticity distribution which leads to the poor and unstable elasticity distribution estimation in the presence of noise. Toward this end, we propose an efficient statistical methodology for physical forward model refinement by formulating it as linear algebraic representation with respect to the unknown elasticity distribution and incorporating an analytical noise model. To solve the subsequent total variation regularized optimization task, we benefit from a fixed-point scheme involving proximal gradient methods. Simulation results of elasticity reconstruction in various SNR conditions verify the effectiveness of the proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge