Optimal Task Order for Continual Learning of Multiple Tasks

Continual learning of multiple tasks remains a major challenge for neural networks. Here, we investigate how task order influences continual learning and propose a strategy for optimizing it. Leveraging a linear teacher-student model with latent factors, we derive an analytical expression relating task similarity and ordering to learning performance. Our analysis reveals two principles that hold under a wide parameter range: (1) tasks should be arranged from the least representative to the most typical, and (2) adjacent tasks should be dissimilar. We validate these rules on both synthetic data and real-world image classification datasets (Fashion-MNIST, CIFAR-10, CIFAR-100), demonstrating consistent performance improvements in both multilayer perceptrons and convolutional neural networks. Our work thus presents a generalizable framework for task-order optimization in task-incremental continual learning.

Disentangling and Mitigating the Impact of Task Similarity for Continual Learning

Continual learning of partially similar tasks poses a challenge for artificial neural networks, as task similarity presents both an opportunity for knowledge transfer and a risk of interference and catastrophic forgetting. However, it remains unclear how task similarity in input features and readout patterns influences knowledge transfer and forgetting, as well as how they interact with common algorithms for continual learning. Here, we develop a linear teacher-student model with latent structure and show analytically that high input feature similarity coupled with low readout similarity is catastrophic for both knowledge transfer and retention. Conversely, the opposite scenario is relatively benign. Our analysis further reveals that task-dependent activity gating improves knowledge retention at the expense of transfer, while task-dependent plasticity gating does not affect either retention or transfer performance at the over-parameterized limit. In contrast, weight regularization based on the Fisher information metric significantly improves retention, regardless of task similarity, without compromising transfer performance. Nevertheless, its diagonal approximation and regularization in the Euclidean space are much less robust against task similarity. We demonstrate consistent results in a permuted MNIST task with latent variables. Overall, this work provides insights into when continual learning is difficult and how to mitigate it.

Optimal quadratic binding for relational reasoning in vector symbolic neural architectures

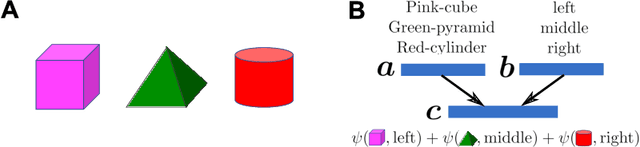
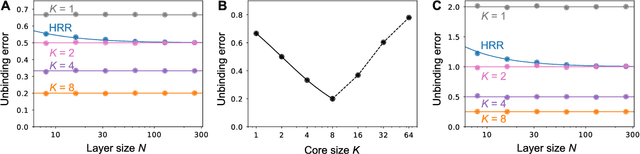
Binding operation is fundamental to many cognitive processes, such as cognitive map formation, relational reasoning, and language comprehension. In these processes, two different modalities, such as location and objects, events and their contextual cues, and words and their roles, need to be bound together, but little is known about the underlying neural mechanisms. Previous works introduced a binding model based on quadratic functions of bound pairs, followed by vector summation of multiple pairs. Based on this framework, we address following questions: Which classes of quadratic matrices are optimal for decoding relational structures? And what is the resultant accuracy? We introduce a new class of binding matrices based on a matrix representation of octonion algebra, an eight-dimensional extension of complex numbers. We show that these matrices enable a more accurate unbinding than previously known methods when a small number of pairs are present. Moreover, numerical optimization of a binding operator converges to this octonion binding. We also show that when there are a large number of bound pairs, however, a random quadratic binding performs as well as the octonion and previously-proposed binding methods. This study thus provides new insight into potential neural mechanisms of binding operations in the brain.