Learning sparse generalized linear models with binary outcomes via iterative hard thresholding

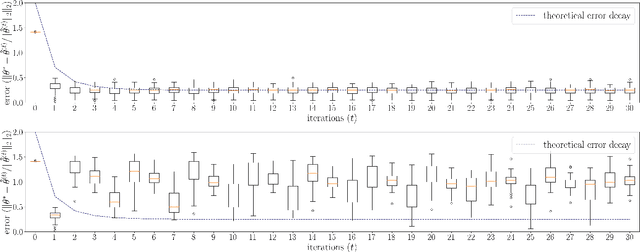
In statistics, generalized linear models (GLMs) are widely used for modeling data and can expressively capture potential nonlinear dependence of the model's outcomes on its covariates. Within the broad family of GLMs, those with binary outcomes, which include logistic and probit regressions, are motivated by common tasks such as binary classification with (possibly) non-separable data. In addition, in modern machine learning and statistics, data is often high-dimensional yet has a low intrinsic dimension, making sparsity constraints in models another reasonable consideration. In this work, we propose to use and analyze an iterative hard thresholding (projected gradient descent on the ReLU loss) algorithm, called binary iterative hard thresholding (BIHT), for parameter estimation in sparse GLMs with binary outcomes. We establish that BIHT is statistically efficient and converges to the correct solution for parameter estimation in a general class of sparse binary GLMs. Unlike many other methods for learning GLMs, including maximum likelihood estimation, generalized approximate message passing, and GLM-tron (Kakade et al. 2011; Bahmani et al. 2016), BIHT does not require knowledge of the GLM's link function, offering flexibility and generality in allowing the algorithm to learn arbitrary binary GLMs. As two applications, logistic and probit regression are additionally studied. In this regard, it is shown that in logistic regression, the algorithm is in fact statistically optimal in the sense that the order-wise sample complexity matches (up to logarithmic factors) the lower bound obtained previously. To the best of our knowledge, this is the first work achieving statistical optimality for logistic regression in all noise regimes with a computationally efficient algorithm. Moreover, for probit regression, our sample complexity is on the same order as that obtained for logistic regression.

Robust 1-bit Compressed Sensing with Iterative Hard Thresholding

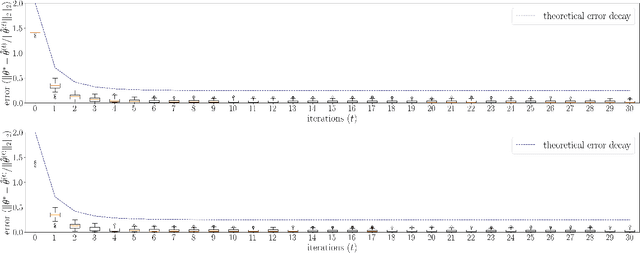
In 1-bit compressed sensing, the aim is to estimate a $k$-sparse unit vector $x\in S^{n-1}$ within an $\epsilon$ error (in $\ell_2$) from minimal number of linear measurements that are quantized to just their signs, i.e., from measurements of the form $y = \mathrm{Sign}(\langle a, x\rangle).$ In this paper, we study a noisy version where a fraction of the measurements can be flipped, potentially by an adversary. In particular, we analyze the Binary Iterative Hard Thresholding (BIHT) algorithm, a proximal gradient descent on a properly defined loss function used for 1-bit compressed sensing, in this noisy setting. It is known from recent results that, with $\tilde{O}(\frac{k}{\epsilon})$ noiseless measurements, BIHT provides an estimate within $\epsilon$ error. This result is optimal and universal, meaning one set of measurements work for all sparse vectors. In this paper, we show that BIHT also provides better results than all known methods for the noisy setting. We show that when up to $\tau$-fraction of the sign measurements are incorrect (adversarial error), with the same number of measurements as before, BIHT agnostically provides an estimate of $x$ within an $\tilde{O}(\epsilon+\tau)$ error, maintaining the universality of measurements. This establishes stability of iterative hard thresholding in the presence of measurement error. To obtain the result, we use the restricted approximate invertibility of Gaussian matrices, as well as a tight analysis of the high-dimensional geometry of the adversarially corrupted measurements.

Improved Support Recovery in Universal One-bit Compressed Sensing

One-bit compressed sensing (1bCS) is an extremely quantized signal acquisition method that has been proposed and studied rigorously in the past decade. In 1bCS, linear samples of a high dimensional signal are quantized to only one bit per sample (sign of the measurement). Assuming the original signal vector to be sparse, existing results in 1bCS either aim to find the support of the vector, or approximate the signal allowing a small error. The focus of this paper is support recovery, which often also computationally facilitate approximate signal recovery. A {\em universal} measurement matrix for 1bCS refers to one set of measurements that work for all sparse signals. With universality, it is known that $\tilde{\Theta}(k^2)$ 1bCS measurements are necessary and sufficient for support recovery (where $k$ denotes the sparsity). To improve the dependence on sparsity from quadratic to linear, in this work we propose approximate support recovery (allowing $\epsilon>0$ proportion of errors), and superset recovery (allowing $\epsilon$ proportion of false positives). We show that the first type of recovery is possible with $\tilde{O}(k/\epsilon)$ measurements, while the later type of recovery, more challenging, is possible with $\tilde{O}(\max\{k/\epsilon,k^{3/2}\})$ measurements. We also show that in both cases $\Omega(k/\epsilon)$ measurements would be necessary for universal recovery. Improved results are possible if we consider universal recovery within a restricted class of signals, such as rational signals, or signals with bounded dynamic range. In both cases superset recovery is possible with only $\tilde{O}(k/\epsilon)$ measurements. Other results on universal but approximate support recovery are also provided in this paper. All of our main recovery algorithms are simple and polynomial-time.

Binary Iterative Hard Thresholding Converges with Optimal Number of Measurements for 1-Bit Compressed Sensing

Compressed sensing has been a very successful high-dimensional signal acquisition and recovery technique that relies on linear operations. However, the actual measurements of signals have to be quantized before storing or processing. 1(One)-bit compressed sensing is a heavily quantized version of compressed sensing, where each linear measurement of a signal is reduced to just one bit: the sign of the measurement. Once enough of such measurements are collected, the recovery problem in 1-bit compressed sensing aims to find the original signal with as much accuracy as possible. The recovery problem is related to the traditional "halfspace-learning" problem in learning theory. For recovery of sparse vectors, a popular reconstruction method from 1-bit measurements is the binary iterative hard thresholding (BIHT) algorithm. The algorithm is a simple projected sub-gradient descent method, and is known to converge well empirically, despite the nonconvexity of the problem. The convergence property of BIHT was not theoretically justified, except with an exorbitantly large number of measurements (i.e., a number of measurement greater than $\max\{k^{10}, 24^{48}, k^{3.5}/\epsilon\}$, where $k$ is the sparsity, $\epsilon$ denotes the approximation error, and even this expression hides other factors). In this paper we show that the BIHT algorithm converges with only $\tilde{O}(\frac{k}{\epsilon})$ measurements. Note that, this dependence on $k$ and $\epsilon$ is optimal for any recovery method in 1-bit compressed sensing. With this result, to the best of our knowledge, BIHT is the only practical and efficient (polynomial time) algorithm that requires the optimal number of measurements in all parameters (both $k$ and $\epsilon$). This is also an example of a gradient descent algorithm converging to the correct solution for a nonconvex problem, under suitable structural conditions.