Numerical solution of a PDE arising from prediction with expert advice

This work investigates the online machine learning problem of prediction with expert advice in an adversarial setting through numerical analysis of, and experiments with, a related partial differential equation. The problem is a repeated two-person game involving decision-making at each step informed by $n$ experts in an adversarial environment. The continuum limit of this game over a large number of steps is a degenerate elliptic equation whose solution encodes the optimal strategies for both players. We develop numerical methods for approximating the solution of this equation in relatively high dimensions ($n\leq 10$) by exploiting symmetries in the equation and the solution to drastically reduce the size of the computational domain. Based on our numerical results we make a number of conjectures about the optimality of various adversarial strategies, in particular about the non-optimality of the COMB strategy.

Consistency of semi-supervised learning, stochastic tug-of-war games, and the p-Laplacian

In this paper we give a broad overview of the intersection of partial differential equations (PDEs) and graph-based semi-supervised learning. The overview is focused on a large body of recent work on PDE continuum limits of graph-based learning, which have been used to prove well-posedness of semi-supervised learning algorithms in the large data limit. We highlight some interesting research directions revolving around consistency of graph-based semi-supervised learning, and present some new results on the consistency of p-Laplacian semi-supervised learning using the stochastic tug-of-war game interpretation of the p-Laplacian. We also present the results of some numerical experiments that illustrate our results and suggest directions for future work.

Asymptotically optimal strategies for online prediction with history-dependent experts

We establish sharp asymptotically optimal strategies for the problem of online prediction with history dependent experts. The prediction problem is played (in part) over a discrete graph called the $d$ dimensional de Bruijn graph, where $d$ is the number of days of history used by the experts. Previous work [11] established $O(\varepsilon)$ optimal strategies for $n=2$ experts and $d\leq 4$ days of history, while [10] established $O(\varepsilon^{1/3})$ optimal strategies for all $n\geq 2$ and all $d\geq 1$, where the game is played for $N$ steps and $\varepsilon=N^{-1/2}$. In this paper, we show that the optimality conditions over the de Bruijn graph correspond to a graph Poisson equation, and we establish $O(\varepsilon)$ optimal strategies for all values of $n$ and $d$.

Online Prediction With History-Dependent Experts: The General Case

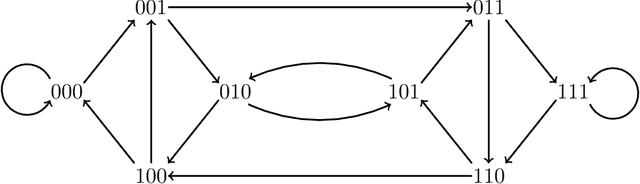
We study the problem of prediction of binary sequences with expert advice in the online setting, which is a classic example of online machine learning. We interpret the binary sequence as the price history of a stock, and view the predictor as an investor, which converts the problem into a stock prediction problem. In this framework, an investor, who predicts the daily movements of a stock, and an adversarial market, who controls the stock, play against each other over $N$ turns. The investor combines the predictions of $n\geq 2$ experts in order to make a decision about how much to invest at each turn, and aims to minimize their regret with respect to the best-performing expert at the end of the game. We consider the problem with history-dependent experts, in which each expert uses the previous $d$ days of history of the market in making their predictions. We prove that the value function for this game, rescaled appropriately, converges as $N\to \infty$ at a rate of $O(N^{-1/6})$ to the viscosity solution of a nonlinear degenerate elliptic PDE, which can be understood as the Hamilton-Jacobi-Issacs equation for the two-person game. As a result, we are able to deduce asymptotically optimal strategies for the investor. Our results extend those established by the first author and R.V.Kohn [13] for $n=2$ experts and $d\leq 4$ days of history.

A PDE Approach to the Prediction of a Binary Sequence with Advice from Two History-Dependent Experts

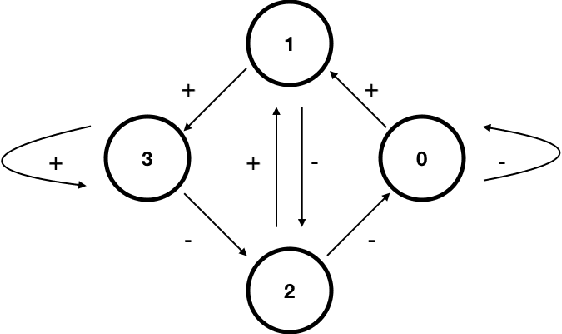
The prediction of a binary sequence is a classic example of online machine learning. We like to call it the 'stock prediction problem,' viewing the sequence as the price history of a stock that goes up or down one unit at each time step. In this problem, an investor has access to the predictions of two or more 'experts,' and strives to minimize her final-time regret with respect to the best-performing expert. Probability plays no role; rather, the market is assumed to be adversarial. We consider the case when there are two history-dependent experts, whose predictions are determined by the d most recent stock moves. Focusing on an appropriate continuum limit and using methods from optimal control, graph theory, and partial differential equations, we discuss strategies for the investor and the adversarial market, and we determine associated upper and lower bounds for the investor's final-time regret. When d is less than 4 our upper and lower bounds coalesce, so the proposed strategies are asymptotically optimal. Compared to other recent applications of partial differential equations to prediction, ours has a new element: there are two timescales, since the recent history changes at every step whereas regret accumulates more slowly.

Prediction with Expert Advice: a PDE Perspective

This work addresses a classic problem of online prediction with expert advice. We assume an adversarial opponent, and we consider both the finite-horizon and random-stopping versions of this zero-sum, two-person game. Focusing on an appropriate continuum limit and using methods from optimal control, we characterize the value of the game as the viscosity solution of a certain nonlinear partial differential equation. The analysis also reveals the predictor's and the opponent's minimax optimal strategies. Our work provides, in particular, a continuum perspective on recent work of Gravin, Peres, and Sivan (Proc SODA 2016). Our techniques are similar to those of Kohn and Serfaty (Comm Pure Appl Math 2010), where scaling limits of some two-person games led to elliptic or parabolic PDEs.