Correlation to Causation: A Causal Deep Learning Framework for Arctic Sea Ice Prediction

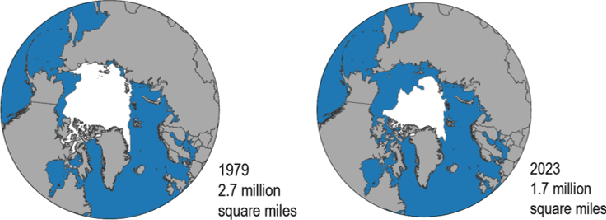
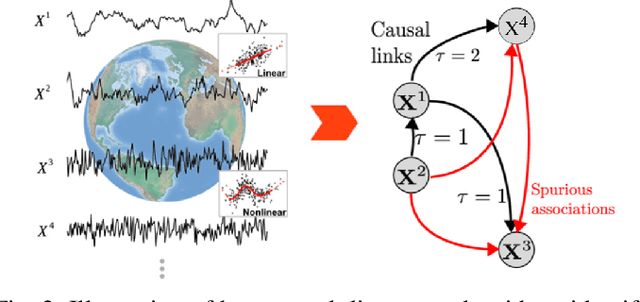
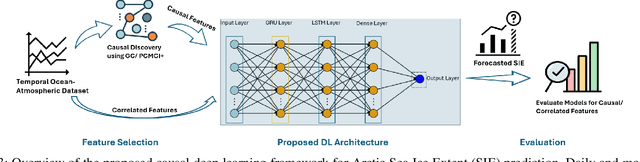
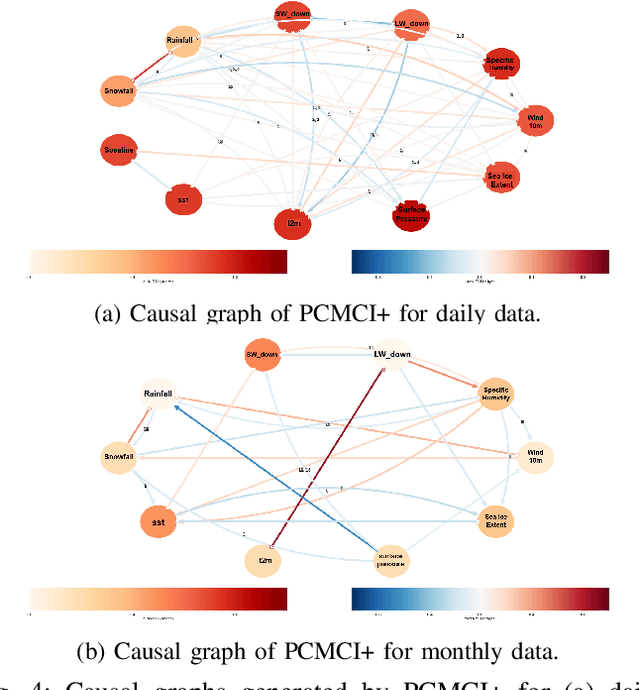
Traditional machine learning and deep learning techniques rely on correlation-based learning, often failing to distinguish spurious associations from true causal relationships, which limits robustness, interpretability, and generalizability. To address these challenges, we propose a causality-driven deep learning framework that integrates Multivariate Granger Causality (MVGC) and PCMCI+ causal discovery algorithms with a hybrid deep learning architecture. Using 43 years (1979-2021) of daily and monthly Arctic Sea Ice Extent (SIE) and ocean-atmospheric datasets, our approach identifies causally significant factors, prioritizes features with direct influence, reduces feature overhead, and improves computational efficiency. Experiments demonstrate that integrating causal features enhances the deep learning model's predictive accuracy and interpretability across multiple lead times. Beyond SIE prediction, the proposed framework offers a scalable solution for dynamic, high-dimensional systems, advancing both theoretical understanding and practical applications in predictive modeling.

eCDANs: Efficient Temporal Causal Discovery from Autocorrelated and Non-stationary Data (Student Abstract)

Conventional temporal causal discovery (CD) methods suffer from high dimensionality, fail to identify lagged causal relationships, and often ignore dynamics in relations. In this study, we present a novel constraint-based CD approach for autocorrelated and non-stationary time series data (eCDANs) capable of detecting lagged and contemporaneous causal relationships along with temporal changes. eCDANs addresses high dimensionality by optimizing the conditioning sets while conducting conditional independence (CI) tests and identifies the changes in causal relations by introducing a surrogate variable to represent time dependency. Experiments on synthetic and real-world data show that eCDANs can identify time influence and outperform the baselines.

CDANs: Temporal Causal Discovery from Autocorrelated and Non-Stationary Time Series Data

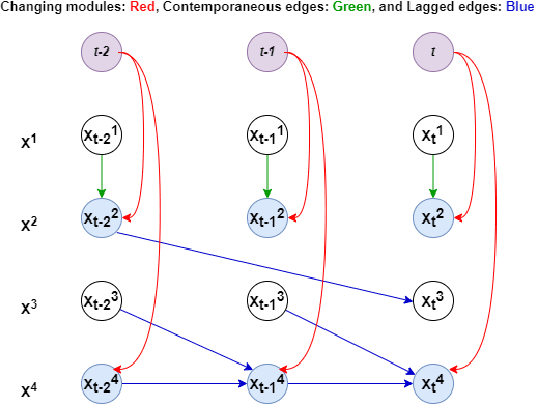
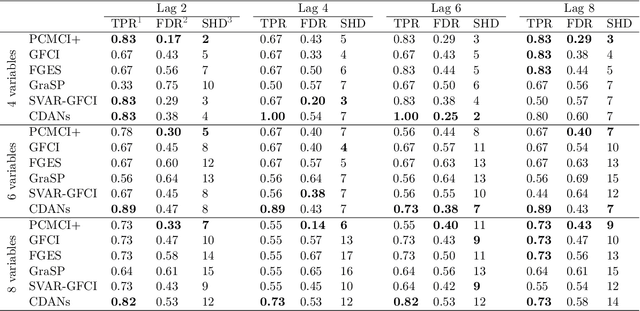
This study presents a novel constraint-based causal discovery approach for autocorrelated and non-stationary time series data (CDANs). Our proposed method addresses several limitations of existing causal discovery methods for autocorrelated and non-stationary time series data, such as high dimensionality, the inability to identify lagged causal relationships, and the overlook of changing modules. Our approach identifies both lagged and instantaneous/contemporaneous causal relationships along with changing modules that vary over time. The method optimizes the conditioning sets in a constraint-based search by considering lagged parents instead of conditioning on the entire past that addresses high dimensionality. The changing modules are detected by considering both contemporaneous and lagged parents. The approach first detects the lagged adjacencies, then identifies the changing modules and contemporaneous adjacencies, and finally determines the causal direction. We extensively evaluated the proposed method using synthetic datasets and a real-world clinical dataset and compared its performance with several baseline approaches. The results demonstrate the effectiveness of the proposed method in detecting causal relationships and changing modules in autocorrelated and non-stationary time series data.