rfPhen2Gen: A machine learning based association study of brain imaging phenotypes to genotypes

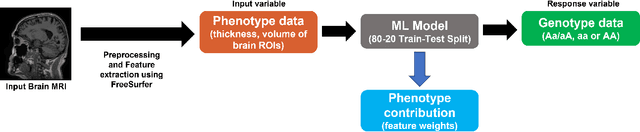
Imaging genetic studies aim to find associations between genetic variants and imaging quantitative traits. Traditional genome-wide association studies (GWAS) are based on univariate statistical tests, but when multiple traits are analyzed together they suffer from a multiple-testing problem and from not taking into account correlations among the traits. An alternative approach to multi-trait GWAS is to reverse the functional relation between genotypes and traits, by fitting a multivariate regression model to predict genotypes from multiple traits simultaneously. However, current reverse genotype prediction approaches are mostly based on linear models. Here, we evaluated random forest regression (RFR) as a method to predict SNPs from imaging QTs and identify biologically relevant associations. We learned machine learning models to predict 518,484 SNPs using 56 brain imaging QTs. We observed that genotype regression error is a better indicator of permutation p-value significance than genotype classification accuracy. SNPs within the known Alzheimer disease (AD) risk gene APOE had lowest RMSE for lasso and random forest, but not ridge regression. Moreover, random forests identified additional SNPs that were not prioritized by the linear models but are known to be associated with brain-related disorders. Feature selection identified well-known brain regions associated with AD,like the hippocampus and amygdala, as important predictors of the most significant SNPs. In summary, our results indicate that non-linear methods like random forests may offer additional insights into phenotype-genotype associations compared to traditional linear multi-variate GWAS methods.

High-dimensional multi-trait GWAS by reverse prediction of genotypes

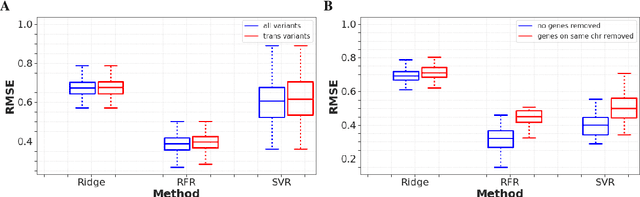
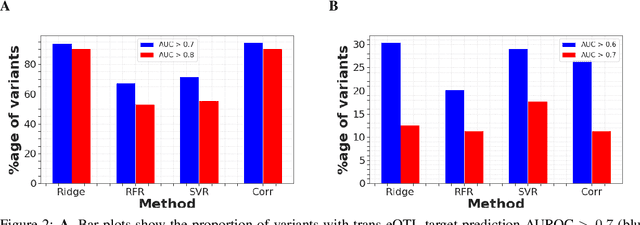
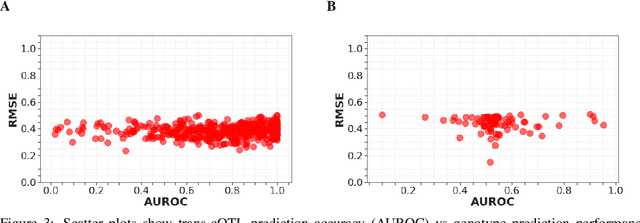
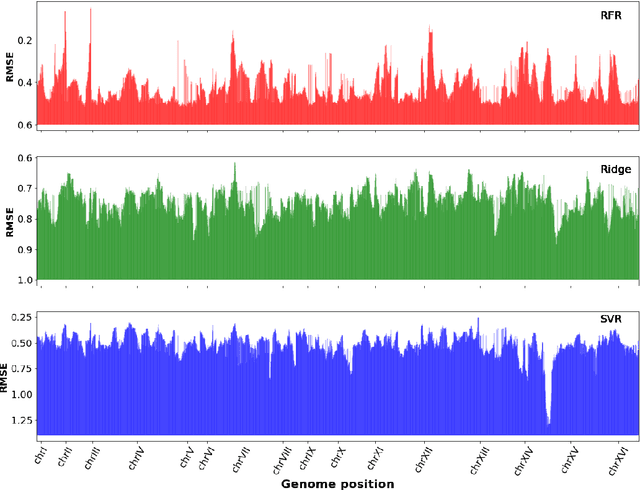
Multi-trait genome-wide association studies (GWAS) use multi-variate statistical methods to identify associations between genetic variants and multiple correlated traits simultaneously, and have higher statistical power than independent univariate analysis of traits. Reverse regression, where genotypes of genetic variants are regressed on multiple traits simultaneously, has emerged as a promising approach to perform multi-trait GWAS in high-dimensional settings where the number of traits exceeds the number of samples. We extended this approach and analyzed different machine learning methods (ridge regression, random forests and support vector machines)for reverse regression in multi-trait GWAS, using genotypes, gene expression data and ground-truth transcriptional regulatory networks from the DREAM5 SysGen Challenge and from a cross between two yeast strains to evaluate methods. We found that genotype prediction performance, in terms of root mean squared error (RMSE), allowed to distinguish between genomic regions with high and low transcriptional activity. Moreover, model feature coefficients correlated with the strength of association between variants and individual traits, and were predictive of true trans-eQTL target genes, with complementary findings across methods.

Restricted maximum-likelihood method for learning latent variance components in gene expression data with known and unknown confounders

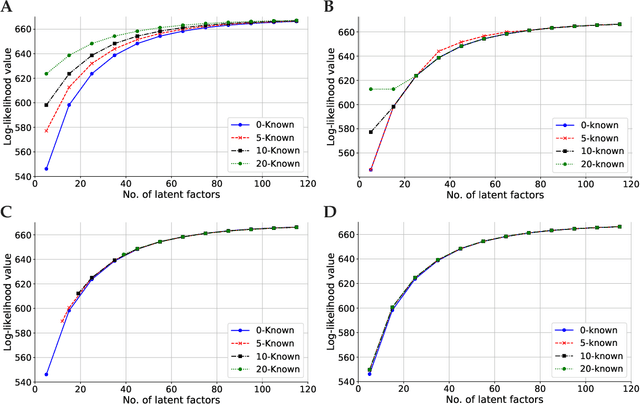
Linear mixed modelling is a popular approach for detecting and correcting spurious sample correlations due to hidden confounders in genome-wide gene expression data. In applications where some confounding factors are known, estimating simultaneously the contribution of known and latent variance components in linear mixed models is a challenge that has so far relied on numerical gradient-based optimizers to maximize the likelihood function. This is unsatisfactory because the resulting solution is poorly characterized and the efficiency of the method may be suboptimal. Here we prove analytically that maximum-likelihood latent variables can always be chosen orthogonal to the known confounding factors, in other words, that maximum-likelihood latent variables explain sample covariances not already explained by known factors. Based on this result we propose a restricted maximum-likelihood method which estimates the latent variables by maximizing the likelihood on the restricted subspace orthogonal to the known confounding factors, and show that this reduces to probabilistic PCA on that subspace. The method then estimates the variance-covariance parameters by maximizing the remaining terms in the likelihood function given the latent variables, using a newly derived analytic solution for this problem. Compared to gradient-based optimizers, our method attains equal or higher likelihood values, can be computed using standard matrix operations, results in latent factors that don't overlap with any known factors, and has a runtime reduced by several orders of magnitude. We anticipate that the restricted maximum-likelihood method will facilitate the application of linear mixed modelling strategies for learning latent variance components to much larger gene expression datasets than currently possible.