Adaptive Long-term Embedding with Denoising and Augmentation for Recommendation

The rapid growth of the internet has made personalized recommendation systems indispensable. Graph-based sequential recommendation systems, powered by Graph Neural Networks (GNNs), effectively capture complex user-item interactions but often face challenges such as noise and static representations. In this paper, we introduce the Adaptive Long-term Embedding with Denoising and Augmentation for Recommendation (ALDA4Rec) method, a novel model that constructs an item-item graph, filters noise through community detection, and enriches user-item interactions. Graph Convolutional Networks (GCNs) are then employed to learn short-term representations, while averaging, GRUs, and attention mechanisms are utilized to model long-term embeddings. An MLP-based adaptive weighting strategy is further incorporated to dynamically optimize long-term user preferences. Experiments conducted on four real-world datasets demonstrate that ALDA4Rec outperforms state-of-the-art baselines, delivering notable improvements in both accuracy and robustness. The source code is available at https://github.com/zahraakhlaghi/ALDA4Rec.

Anchor-based oversampling for imbalanced tabular data via contrastive and adversarial learning

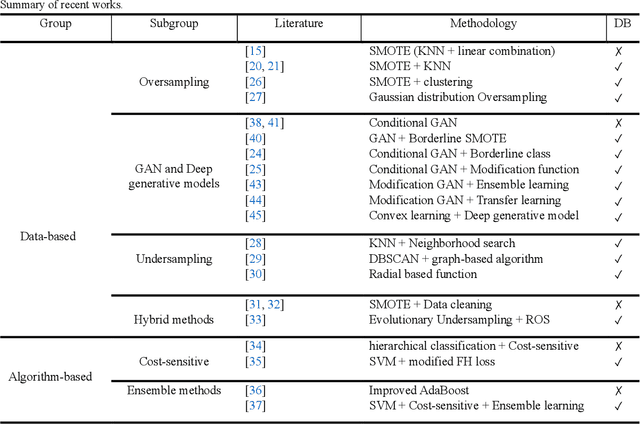
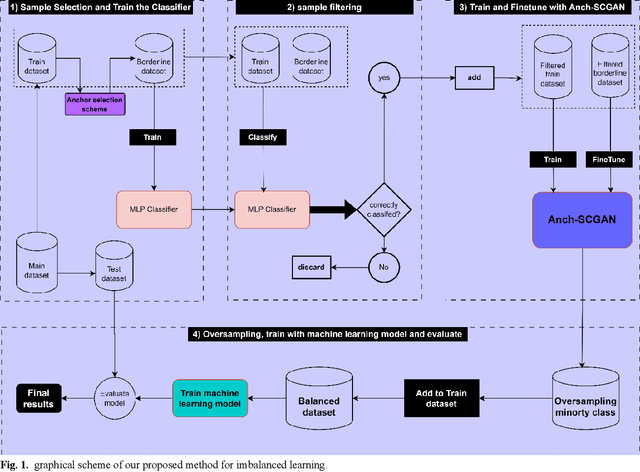
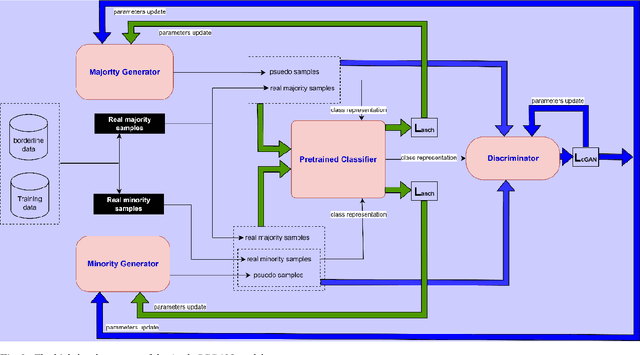
Imbalanced data represent a distribution with more frequencies of one class (majority) than the other (minority). This phenomenon occurs across various domains, such as security, medical care and human activity. In imbalanced learning, classification algorithms are typically inclined to classify the majority class accurately, resulting in artificially high accuracy rates. As a result, many minority samples are mistakenly labelled as majority-class instances, resulting in a bias that benefits the majority class. This study presents a framework based on boundary anchor samples to tackle the imbalance learning challenge. First, we select and use anchor samples to train a multilayer perceptron (MLP) classifier, which acts as a prior knowledge model and aids the adversarial and contrastive learning procedures. Then, we designed a novel deep generative model called Anchor Stabilized Conditional Generative Adversarial Network or Anch-SCGAN in short. Anch-SCGAN is supported with two generators for the minority and majority classes and a discriminator incorporating additional class-specific information from the pre-trained feature extractor MLP. In addition, we facilitate the generator's training procedure in two ways. First, we define a new generator loss function based on reprocessed anchor samples and contrastive learning. Second, we apply a scoring strategy to stabilize the adversarial training part in generators. We train Anch-SCGAN and further finetune it with anchor samples to improve the precision of the generated samples. Our experiments on 16 real-world imbalanced datasets illustrate that Anch-SCGAN outperforms the renowned methods in imbalanced learning.

Neighborhood-Order Learning Graph Attention Network for Fake News Detection

Fake news detection is a significant challenge in the digital age, which has become increasingly important with the proliferation of social media and online communication networks. Graph Neural Networks (GNN)-based methods have shown high potential in analyzing graph-structured data for this problem. However, a major limitation in conventional GNN architectures is their inability to effectively utilize information from neighbors beyond the network's layer depth, which can reduce the model's accuracy and effectiveness. In this paper, we propose a novel model called Neighborhood-Order Learning Graph Attention Network (NOL-GAT) for fake news detection. This model allows each node in each layer to independently learn its optimal neighborhood order. By doing so, the model can purposefully and efficiently extract critical information from distant neighbors. The NOL-GAT architecture consists of two main components: a Hop Network that determines the optimal neighborhood order and an Embedding Network that updates node embeddings using these optimal neighborhoods. To evaluate the model's performance, experiments are conducted on various fake news datasets. Results demonstrate that NOL-GAT significantly outperforms baseline models in metrics such as accuracy and F1-score, particularly in scenarios with limited labeled data. Features such as mitigating the over-squashing problem, improving information flow, and reducing computational complexity further highlight the advantages of the proposed model.

A Decision-Based Heterogenous Graph Attention Network for Multi-Class Fake News Detection

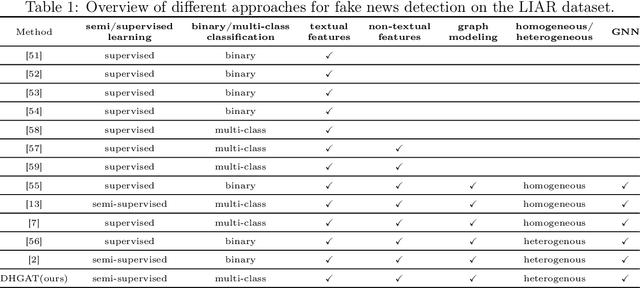
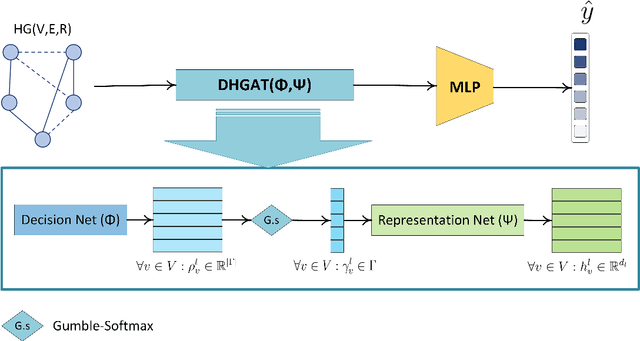
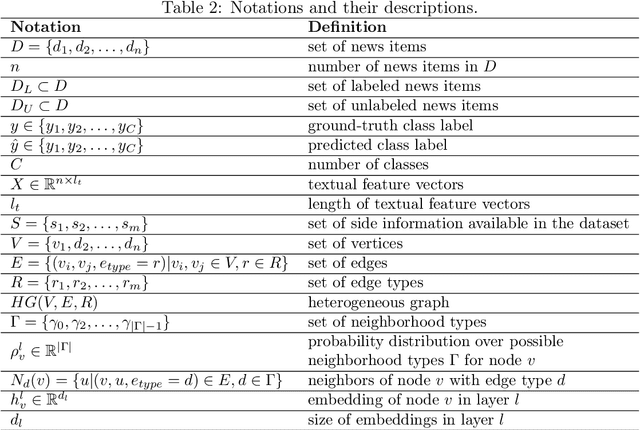
A promising tool for addressing fake news detection is Graph Neural Networks (GNNs). However, most existing GNN-based methods rely on binary classification, categorizing news as either real or fake. Additionally, traditional GNN models use a static neighborhood for each node, making them susceptible to issues like over-squashing. In this paper, we introduce a novel model named Decision-based Heterogeneous Graph Attention Network (DHGAT) for fake news detection in a semi-supervised setting. DHGAT effectively addresses the limitations of traditional GNNs by dynamically optimizing and selecting the neighborhood type for each node in every layer. It represents news data as a heterogeneous graph where nodes (news items) are connected by various types of edges. The architecture of DHGAT consists of a decision network that determines the optimal neighborhood type and a representation network that updates node embeddings based on this selection. As a result, each node learns an optimal and task-specific computational graph, enhancing both the accuracy and efficiency of the fake news detection process. We evaluate DHGAT on the LIAR dataset, a large and challenging dataset for multi-class fake news detection, which includes news items categorized into six classes. Our results demonstrate that DHGAT outperforms existing methods, improving accuracy by approximately 4% and showing robustness with limited labeled data.

LOSS-GAT: Label Propagation and One-Class Semi-Supervised Graph Attention Network for Fake News Detection

In the era of widespread social networks, the rapid dissemination of fake news has emerged as a significant threat, inflicting detrimental consequences across various dimensions of people's lives. Machine learning and deep learning approaches have been extensively employed for identifying fake news. However, a significant challenge in identifying fake news is the limited availability of labeled news datasets. Therefore, the One-Class Learning (OCL) approach, utilizing only a small set of labeled data from the interest class, can be a suitable approach to address this challenge. On the other hand, representing data as a graph enables access to diverse content and structural information, and label propagation methods on graphs can be effective in predicting node labels. In this paper, we adopt a graph-based model for data representation and introduce a semi-supervised and one-class approach for fake news detection, called LOSS-GAT. Initially, we employ a two-step label propagation algorithm, utilizing Graph Neural Networks (GNNs) as an initial classifier to categorize news into two groups: interest (fake) and non-interest (real). Subsequently, we enhance the graph structure using structural augmentation techniques. Ultimately, we predict the final labels for all unlabeled data using a GNN that induces randomness within the local neighborhood of nodes through the aggregation function. We evaluate our proposed method on five common datasets and compare the results against a set of baseline models, including both OCL and binary labeled models. The results demonstrate that LOSS-GAT achieves a notable improvement, surpassing 10%, with the advantage of utilizing only a limited set of labeled fake news. Noteworthy, LOSS-GAT even outperforms binary labeled models.

Heterophily-Aware Fair Recommendation using Graph Convolutional Networks

In recent years, graph neural networks (GNNs) have become a popular tool to improve the accuracy and performance of recommender systems. Modern recommender systems are not only designed to serve the end users, but also to benefit other participants, such as items and items providers. These participants may have different or conflicting goals and interests, which raise the need for fairness and popularity bias considerations. GNN-based recommendation methods also face the challenges of unfairness and popularity bias and their normalization and aggregation processes suffer from these challenges. In this paper, we propose a fair GNN-based recommender system, called HetroFair, to improve items' side fairness. HetroFair uses two separate components to generate fairness-aware embeddings: i) fairness-aware attention which incorporates dot product in the normalization process of GNNs, to decrease the effect of nodes' degrees, and ii) heterophily feature weighting to assign distinct weights to different features during the aggregation process. In order to evaluate the effectiveness of HetroFair, we conduct extensive experiments over six real-world datasets. Our experimental results reveal that HetroFair not only alleviates the unfairness and popularity bias on the items' side, but also achieves superior accuracy on the users' side. Our implementation is publicly available at https://github.com/NematGH/HetroFair

Strong Transitivity Relations and Graph Neural Networks

Local neighborhoods play a crucial role in embedding generation in graph-based learning. It is commonly believed that nodes ought to have embeddings that resemble those of their neighbors. In this research, we try to carefully expand the concept of similarity from nearby neighborhoods to the entire graph. We provide an extension of similarity that is based on transitivity relations, which enables Graph Neural Networks (GNNs) to capture both global similarities and local similarities over the whole graph. We introduce Transitivity Graph Neural Network (TransGNN), which more than local node similarities, takes into account global similarities by distinguishing strong transitivity relations from weak ones and exploiting them. We evaluate our model over several real-world datasets and showed that it considerably improves the performance of several well-known GNN models, for tasks such as node classification.

Content Augmented Graph Neural Networks

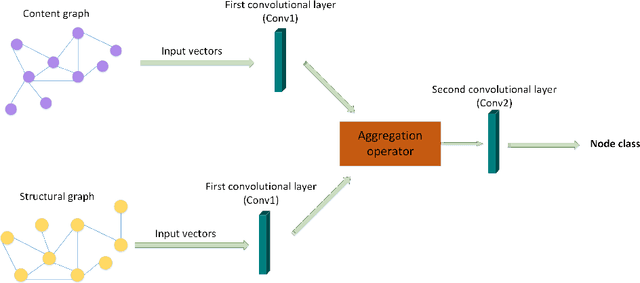
In recent years, graph neural networks (GNNs) have become a popular tool for solving various problems over graphs. In these models, the link structure of the graph is typically exploited and nodes' embeddings are iteratively updated based on adjacent nodes. Nodes' contents are used solely in the form of feature vectors, served as nodes' first-layer embeddings. However, the filters or convolutions, applied during iterations/layers to these initial embeddings lead to their impact diminish and contribute insignificantly to the final embeddings. In order to address this issue, in this paper we propose augmenting nodes' embeddings by embeddings generating from their content, at higher GNN layers. More precisely, we propose models wherein a structural embedding using a GNN and a content embedding are computed for each node. These two are combined using a combination layer to form the embedding of a node at a given layer. We suggest methods such as using an auto-encoder or building a content graph, to generate content embeddings. In the end, by conducting experiments over several real-world datasets, we demonstrate the high accuracy and performance of our models.

The Embeddings World and Artificial General Intelligence

From early days, a key and controversial question inside the artificial intelligence community was whether Artificial General Intelligence (AGI) is achievable. AGI is the ability of machines and computer programs to achieve human-level intelligence and do all tasks that a human being can. While there exist a number of systems in the literature claiming they realize AGI, several other researchers argue that it is impossible to achieve it. In this paper, we take a different view to the problem. First, we discuss that in order to realize AGI, along with building intelligent machines and programs, an intelligent world should also be constructed which is on the one hand, an accurate approximation of our world and on the other hand, a significant part of reasoning of intelligent machines is already embedded in this world. Then we discuss that AGI is not a product or algorithm, rather it is a continuous process which will become more and more mature over time (like human civilization and wisdom). Then, we argue that pre-trained embeddings play a key role in building this intelligent world and as a result, realizing AGI. We discuss how pre-trained embeddings facilitate achieving several characteristics of human-level intelligence, such as embodiment, common sense knowledge, unconscious knowledge and continuality of learning, by machines.

Sketch-based Randomized Algorithms for Dynamic Graph Regression

A well-known problem in data science and machine learning is {\em linear regression}, which is recently extended to dynamic graphs. Existing exact algorithms for updating the solution of dynamic graph regression problem require at least a linear time (in terms of $n$: the size of the graph). However, this time complexity might be intractable in practice. In the current paper, we utilize {\em subsampled randomized Hadamard transform} and \textsf{CountSketch} to propose the first randomized algorithms. Suppose that we are given an $n\times m$ matrix embedding $M$ of the graph, where $m \ll n$. Let $r$ be the number of samples required for a guaranteed approximation error, which is a sublinear function of $n$. Our first algorithm reduces time complexity of pre-processing to $O(n(m + 1) + 2n(m + 1) \log_2(r + 1) + rm^2)$. Then after an edge insertion or an edge deletion, it updates the approximate solution in $O(rm)$ time. Our second algorithm reduces time complexity of pre-processing to $O \left( nnz(M) + m^3 \epsilon^{-2} \log^7(m/\epsilon) \right)$, where $nnz(M)$ is the number of nonzero elements of $M$. Then after an edge insertion or an edge deletion or a node insertion or a node deletion, it updates the approximate solution in $O(qm)$ time, with $q=O\left(\frac{m^2}{\epsilon^2} \log^6(m/\epsilon) \right)$. Finally, we show that under some assumptions, if $\ln n < \epsilon^{-1}$ our first algorithm outperforms our second algorithm and if $\ln n \geq \epsilon^{-1}$ our second algorithm outperforms our first algorithm.