Physics-informed DeepONet with stiffness-based loss functions for structural response prediction

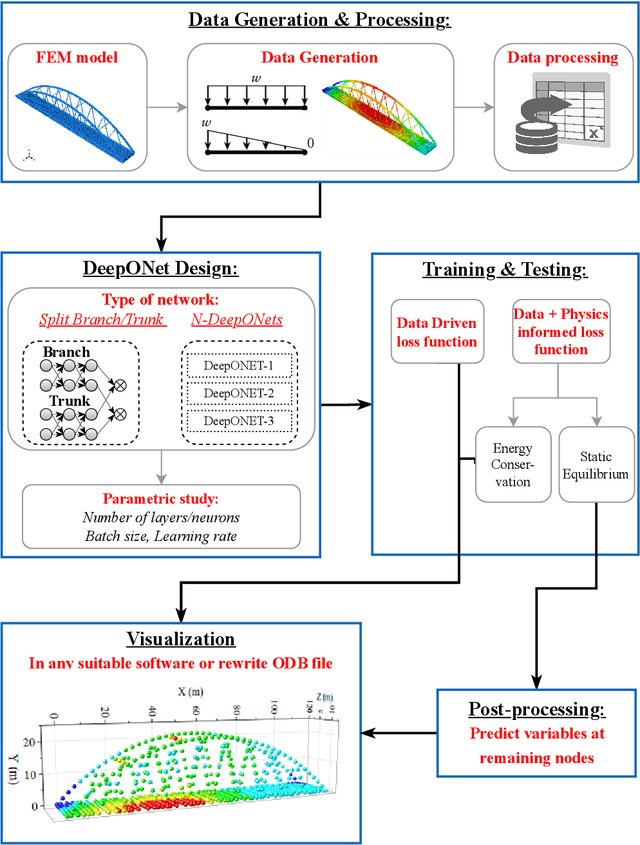
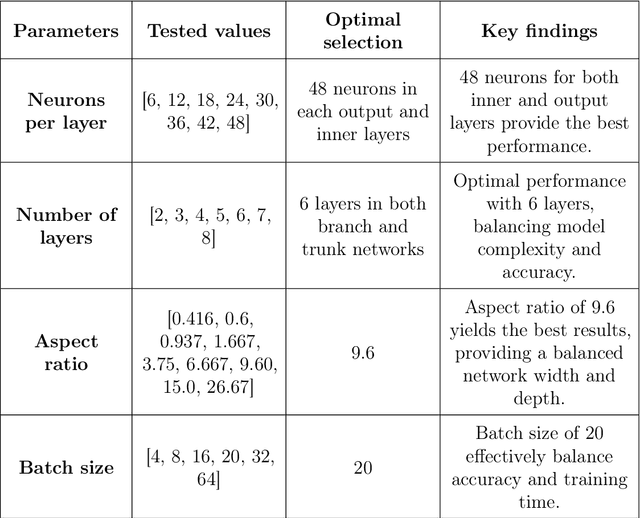
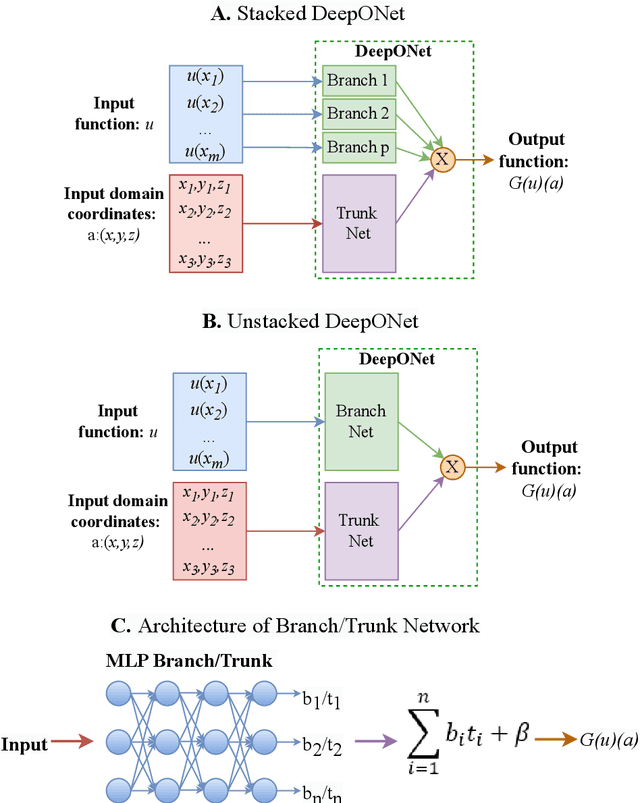
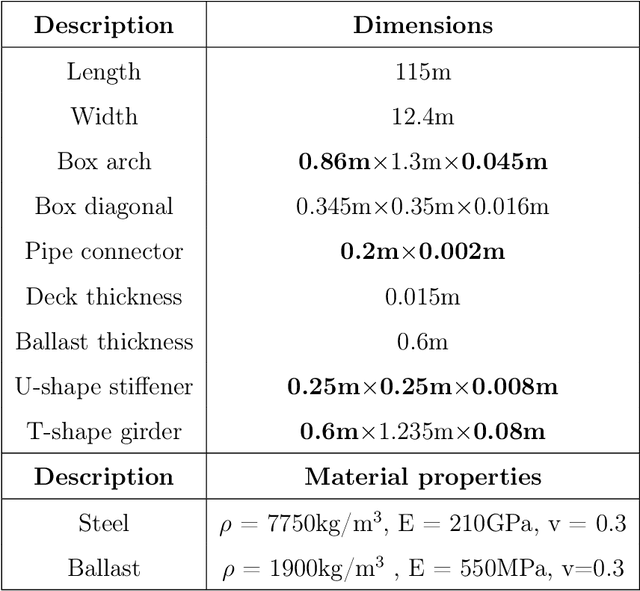
Finite element modeling is a well-established tool for structural analysis, yet modeling complex structures often requires extensive pre-processing, significant analysis effort, and considerable time. This study addresses this challenge by introducing an innovative method for real-time prediction of structural static responses using DeepOnet which relies on a novel approach to physics-informed networks driven by structural balance laws. This approach offers the flexibility to accurately predict responses under various load classes and magnitudes. The trained DeepONet can generate solutions for the entire domain, within a fraction of a second. This capability effectively eliminates the need for extensive remodeling and analysis typically required for each new case in FE modeling. We apply the proposed method to two structures: a simple 2D beam structure and a comprehensive 3D model of a real bridge. To predict multiple variables with DeepONet, we utilize two strategies: a split branch/trunk and multiple DeepONets combined into a single DeepONet. In addition to data-driven training, we introduce a novel physics-informed training approaches. This method leverages structural stiffness matrices to enforce fundamental equilibrium and energy conservation principles, resulting in two novel physics-informed loss functions: energy conservation and static equilibrium using the Schur complement. We use various combinations of loss functions to achieve an error rate of less than 5% with significantly reduced training time. This study shows that DeepONet, enhanced with hybrid loss functions, can accurately and efficiently predict displacements and rotations at each mesh point, with reduced training time.

Damage identification for bridges using machine learning: Development and application to KW51 bridge

Over the past few decades, structural health monitoring (SHM) has drawn significant attention to identifying damage in structures. However, there are open challenges related to the efficiency and applicability of the existing damage identification approaches. This paper proposes an effective approach that integrates both modal analysis and dynamic analysis strategies for damage identification and applies it to the KW51 railway bridge in Leuven, Belgium. The ML-based damage identification utilizes four types of features: modal analysis input, frequency characteristics, time-frequency characteristics, and stacked time series feature extraction from forced acceleration response. Signal processing methods such as stacking, Fourier transform, and wavelet transform are employed to extract damage-sensitive features from the acceleration series. The ML methods, including the k-nearest neighbors (kNN) algorithm, stacked gated recurrent unit (stacked GRU) network, and convolutional neural network (CNN), are then combined to assess the existence, extent, and location of damage. The proposed method is applied to the KW51 railway bridge. A finite element model (FEM) of the KW51 bridge is developed, which is validated by modal analysis. Various extents and locations of damage are simulated to generate the "Damaged" data, while the "Intact" data from FEM or measured data serve as a baseline for comparison. The identification results for the KW51 bridge demonstrate the high accuracy and robustness of the proposed approach, confirming its effectiveness in damage identification problems.

Error convergence and engineering-guided hyperparameter search of PINNs: towards optimized I-FENN performance

In this paper, we aim at enhancing the performance of our proposed I-FENN approach by focusing on two crucial aspects of its PINN component: the error convergence analysis and the hyperparameter-performance relationship. By building on the I-FENN setup, our methodology relies on systematic engineering-oriented numerical analysis that is guided by the available mathematical theories on the topic. The objectivity of the characterization is achieved through a novel combination of performance metrics that asses the success of minimization of various error measures, the training efficiency through optimization process, and the training computational effort. In the first objective, we investigate in detail the convergence of the PINN training error and the global error against the network size and the training sample size. We demonstrate a consistent converging behavior of the two error types, which proves the conformance of the PINN setup and implementation to the available convergence theories. In the second objective, we aim to establish an a-priori knowledge of the hyperparameters which favor higher predictive accuracy, lower computational effort, and the least chances of arriving at trivial solutions. We show that shallow-and-wide networks tend to overestimate high frequencies of the strain field and they are computationally more demanding in the L-BFGS stage. On the other hand, deep-and-narrow PINNs yield higher errors; they are computationally slower during Adam optimization epochs, and they are more prone to training failure by arriving at trivial solutions. Our analysis leads to several outcomes that contribute to the better performance of I-FENN and fills a long-standing gap in the PINN literature with regards to the numerical convergence of the network errors. The proposed analysis method and conclusions can be directly extended to other ML applications in science and engineering.