Moritz Schöfl
Exploring Visual Patterns in Projected Human and Machine Decision-Making Paths
Jan 20, 2020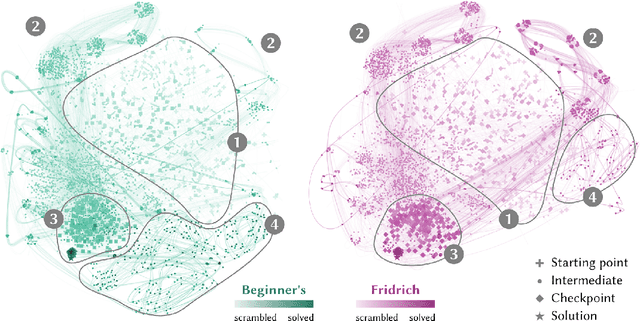


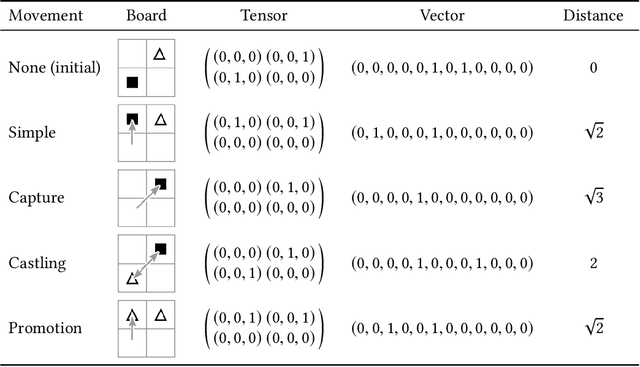
Abstract:In problem solving, the paths towards solutions can be viewed as a sequence of decisions. The decisions, made by humans or computers, describe a trajectory through a high-dimensional representation space of the problem. Using dimensionality reduction, these trajectories can be visualized in lower dimensional space. Such embedded trajectories have previously been applied to a wide variety of data, but so far, almost exclusively the self-similarity of single trajectories has been analyzed. In contrast, we describe patterns emerging from drawing many trajectories---for different initial conditions, end states, or solution strategies---in the same embedding space. We argue that general statements about the problem solving tasks and solving strategies can be made by interpreting these patterns. We explore and characterize such patterns in trajectories resulting from human and machine-made decisions in a variety of application domains: logic puzzles (Rubik's cube), strategy games (chess), and optimization problems (neural network training). In the context of Rubik's cube, we present a physical interactive demonstrator that uses trajectory visualization to provide immediate feedback to users regarding the consequences of their decisions. We also discuss the importance of suitably chosen representation spaces and similarity metrics for the embedding.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge