Data-Driven Observability Analysis for Nonlinear Stochastic Systems

Distinguishability and, by extension, observability are key properties of dynamical systems. Establishing these properties is challenging, especially when no analytical model is available and they are to be inferred directly from measurement data. The presence of noise further complicates this analysis, as standard notions of distinguishability are tailored to deterministic systems. We build on distributional distinguishability, which extends the deterministic notion by comparing distributions of outputs of stochastic systems. We first show that both concepts are equivalent for a class of systems that includes linear systems. We then present a method to assess and quantify distributional distinguishability from output data. Specifically, our quantification measures how much data is required to tell apart two initial states, inducing a continuous spectrum of distinguishability. We propose a statistical test to determine a threshold above which two states can be considered distinguishable with high confidence. We illustrate these tools by computing distinguishability maps over the state space in simulation, then leverage the test to compare sensor configurations on hardware.

Learning dynamics from partial observations with structured neural ODEs

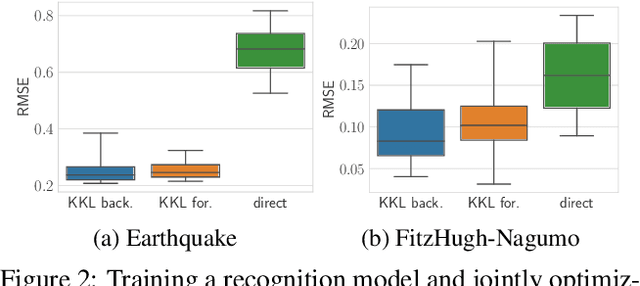
Identifying dynamical systems from experimental data is a notably difficult task. Prior knowledge generally helps, but the extent of this knowledge varies with the application, and customized models are often needed. We propose a flexible framework to incorporate a broad spectrum of physical insight into neural ODE-based system identification, giving physical interpretability to the resulting latent space. This insight is either enforced through hard constraints in the optimization problem or added in its cost function. In order to link the partial and possibly noisy observations to the latent state, we rely on tools from nonlinear observer theory to build a recognition model. We demonstrate the performance of the proposed approach on numerical simulations and on an experimental dataset from a robotic exoskeleton.

Actively Learning Gaussian Process Dynamics

Despite the availability of ever more data enabled through modern sensor and computer technology, it still remains an open problem to learn dynamical systems in a sample-efficient way. We propose active learning strategies that leverage information-theoretical properties arising naturally during Gaussian process regression, while respecting constraints on the sampling process imposed by the system dynamics. Sample points are selected in regions with high uncertainty, leading to exploratory behavior and data-efficient training of the model. All results are finally verified in an extensive numerical benchmark.