A quantum system control method based on enhanced reinforcement learning

Traditional quantum system control methods often face different constraints, and are easy to cause both leakage and stochastic control errors under the condition of limited resources. Reinforcement learning has been proved as an efficient way to complete the quantum system control task. To learn a satisfactory control strategy under the condition of limited resources, a quantum system control method based on enhanced reinforcement learning (QSC-ERL) is proposed. The states and actions in reinforcement learning are mapped to quantum states and control operations in quantum systems. By using new enhanced neural networks, reinforcement learning can quickly achieve the maximization of long-term cumulative rewards, and a quantum state can be evolved accurately from an initial state to a target state. According to the number of candidate unitary operations, the three-switch control is used for simulation experiments. Compared with other methods, the QSC-ERL achieves close to 1 fidelity learning control of quantum systems, and takes fewer episodes to quantum state evolution under the condition of limited resources.

Autonomous Quantum Perceptron Neural Network

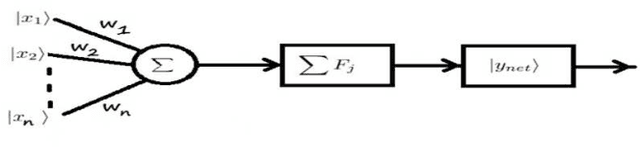
Recently, with the rapid development of technology, there are a lot of applications require to achieve low-cost learning. However the computational power of classical artificial neural networks, they are not capable to provide low-cost learning. In contrast, quantum neural networks may be representing a good computational alternate to classical neural network approaches, based on the computational power of quantum bit (qubit) over the classical bit. In this paper we present a new computational approach to the quantum perceptron neural network can achieve learning in low-cost computation. The proposed approach has only one neuron can construct self-adaptive activation operators capable to accomplish the learning process in a limited number of iterations and, thereby, reduce the overall computational cost. The proposed approach is capable to construct its own set of activation operators to be applied widely in both quantum and classical applications to overcome the linearity limitation of classical perceptron. The computational power of the proposed approach is illustrated via solving variety of problems where promising and comparable results are given.