Noise reduction in ISAR imaging of UAVs using weighted atomic norm minimization and 2D-ADMM algorithm

The effect of noise on the Inverse Synthetic Aperture Radar (ISAR) with sparse apertures is a challenging issue for image reconstruction with high resolution at low Signal-to-Noise Ratios (SNRs). It is well-known that the image resolution is affected by the bandwidth of the transmitted signal and the Coherent Processing Interval (CPI) in two dimensions, range and azimuth, respectively. To reduce the noise effect and thus increase the two-dimensional resolution of Unmanned Aerial Vehicles (UAVs) images, we propose the Fast Reweighted Atomic Norm Denoising (FRAND) algorithm by incorporating the weighted atomic norm minimization. To solve the problem, the Two-Dimensional Alternating Direction Method of Multipliers (2D-ADMM) algorithm is developed to speed up the implementation procedure. Assuming sparse apertures for ISAR images of UAVs, we compare the proposed method with the MUltiple SIgnal Classification (MUSIC), Cadzow, and SL0 methods in different SNRs. Simulation results show the superiority of FRAND at low SNRs based on the Mean-Square Error (MSE), Peak Signal-to-Noise ratio (PSNR) and Structural Similarity Index Measure (SSIM) criteria.

Two-dimensional gridless super-resolution method for ISAR imaging

We are focused on improving the resolution of images of moving targets in Inverse Synthetic Aperture Radar (ISAR) imaging. This could be achieved by recovering the scattering points of a target that have stronger reflections than other target points, leading to increasing the higher Radar Cross Section (RCS) of a target. These points, however, are sparse and when the received data is incomplete, moving targets would not be properly recognizable in ISAR images. To increase the resolution in ISAR imaging, we propose the 2-Dimensional Reweighted Trace Minimization (2D-RWTM) method to retrieve frequencies of sparse scattering points in both range and cross-range directions. This method is a gridless super-resolution method, which does not depend on fitting the scattering point on the grids, leading to less complexity compared to the other methods. Using computer simulations, the proposed 2D-RWTM is compared to the Atomic Norm Minimization (ANM) in terms of the Mean Squared Errors (MSE). The results show that using the proposed method, the scattering points of a target are successfully recovered. It is shown that by selecting different weighting matrices and scattering points adjacent to each other, the recovery in ISAR imaging is still successful.

Fast and Low-Memory Deep Neural Networks Using Binary Matrix Factorization

Despite the outstanding performance of deep neural networks in different applications, they are still computationally extensive and require a great number of memories. This motivates more research on reducing the resources required for implementing such networks. An efficient approach addressed for this purpose is matrix factorization, which has been shown to be effective on different networks. In this paper, we utilize binary matrix factorization and show its great efficiency in reducing the required number of resources in deep neural networks. In effect, this technique can lead to the practical implementation of such networks.

Joint Power and Gain Allocation in MDM-WDM Optical Communication Networks Based on Enhanced Gaussian Noise Model

Achieving reliable communication over different channels and modes is one of the main goals of Mode Division Multiplexing-Wavelength Division Multiplexing (MDM-WDM) communication networks. The reliability can be described by minimum Signal to Noise Ratio (SNR) margin which dependents on launched power, Multimode-Erbium Doped Fiber Amplification (MM-EDFA) gain, and MMF nonlinearity. In this paper, an analytical model for MMF nonlinearity is derived based on Enhanced Gaussian Noise (EGN) model formulation by considering carrier phase estimation and the first four dispersion terms. The proposed EGN model is verified through the split step Fourier method simulation. Considering a multi-node linear network, the joint optimized power and gain allocation based on minimum SNR margin maximization is formulated. The practical constraints including MM-EDFA saturation power and maximum gain are considered and the problem is solved by using convex optimization. Three scenarios are assumed including best equal power, optimized power, and joint optimized power and gain. In the first scenario, equal powers are considered for different channels and modes with equal MM-EDFA gain in all spans. It is worth mentioning that the MM-EDFA gain is equal to span loss. In the second scenario, different powers are allocated to different channels and modes with equal MM-EDFA gain in all spans. In the third case, allocated powers to each channel and mode are optimized. Moreover, the MM-EDFA gain for each span is optimized separately.

Tensor Laplacian Regularized Low-Rank Representation for Non-uniformly Distributed Data Subspace Clustering

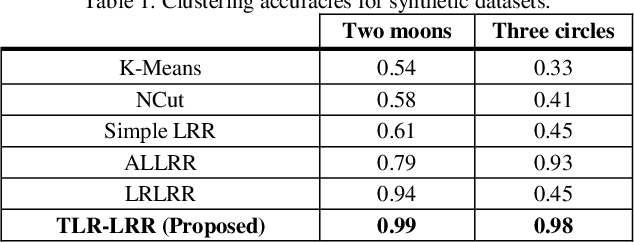
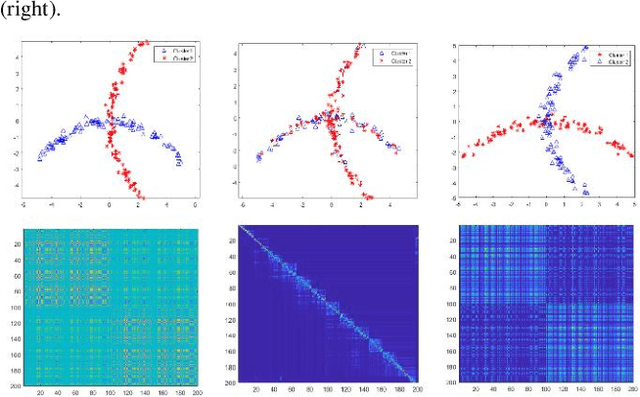
Low-Rank Representation (LRR) highly suffers from discarding the locality information of data points in subspace clustering, as it may not incorporate the data structure nonlinearity and the non-uniform distribution of observations over the ambient space. Thus, the information of the observational density is lost by the state-of-art LRR models, as they take a constant number of adjacent neighbors into account. This, as a result, degrades the subspace clustering accuracy in such situations. To cope with deficiency, in this paper, we propose to consider a hypergraph model to facilitate having a variable number of adjacent nodes and incorporating the locality information of the data. The sparsity of the number of subspaces is also taken into account. To do so, an optimization problem is defined based on a set of regularization terms and is solved by developing a tensor Laplacian-based algorithm. Extensive experiments on artificial and real datasets demonstrate the higher accuracy and precision of the proposed method in subspace clustering compared to the state-of-the-art methods. The outperformance of this method is more revealed in presence of inherent structure of the data such as nonlinearity, geometrical overlapping, and outliers.

Low-Rank Isomap Algorithm

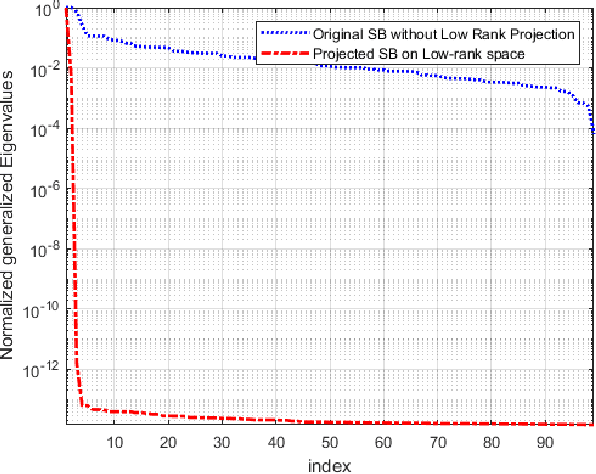
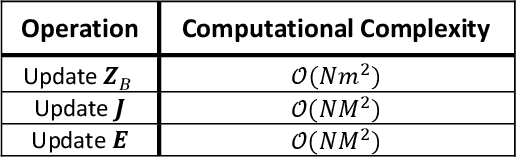
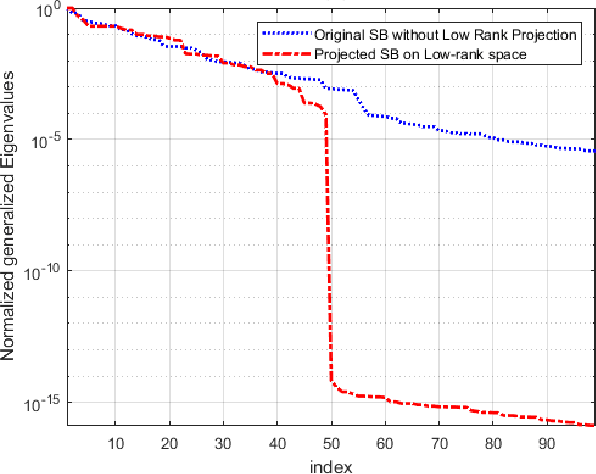
The Isomap is a well-known nonlinear dimensionality reduction method that highly suffers from computational complexity. Its computational complexity mainly arises from two stages; a) embedding a full graph on the data in the ambient space, and b) a complete eigenvalue decomposition. Although the reduction of the computational complexity of the graphing stage has been investigated, yet the eigenvalue decomposition stage remains a bottleneck in the problem. In this paper, we propose the Low-Rank Isomap algorithm by introducing a projection operator on the embedded graph from the ambient space to a low-rank latent space to facilitate applying the partial eigenvalue decomposition. This approach leads to reducing the complexity of Isomap to a linear order while preserving the structural information during the dimensionality reduction process. The superiority of the Low-Rank Isomap algorithm compared to some state-of-art algorithms is experimentally verified on facial image clustering in terms of speed and accuracy.

Super-resolution Method for Coherent DOA Estimation of Multiple Wideband Sources

We focus on coherent direction of arrival estimation of wideband sources based on spatial sparsity. This area of research is encountered in many applications such as passive radar, sonar, mining, and communication problems, in which an increasing attention has been devoted to improving the estimation accuracy and robustness to noise. By the development of super-resolution algorithms, narrowband direction of arrival estimation based on gridless sparse algorithms and atomic norm minimization has already been addressed. In this paper, a superresolution based method is proposed for coherent direction of arrival estimation of multiple wideband sources. First, unlike the conventional coherent methods, we develop a new focusing method to map the subband with the largest center frequency to the other ones, which leads to an accurate method with no requirement for initial estimates for DOAs. Then, we introduce an atomic norm problem by defining a new set of atoms and exploiting the signal joint sparsity of different frequency subbands in a continuous spatial domain. This problem is then cast as a semidefinite program, which leads to implementing a new coherent direction of arrival estimation method with higher resolution and more robustness to noise. Our method needs only one single snapshot for each frequency subband, leading to a small number of snapshots for the received wideband signal compared to the other coherent DOA techniques. Numerical simulations show the outperformance of the proposed method compared to the conventional ones.

Deep Reinforcement Learning-based Anti-jamming Power Allocation in a Two-cell NOMA Network

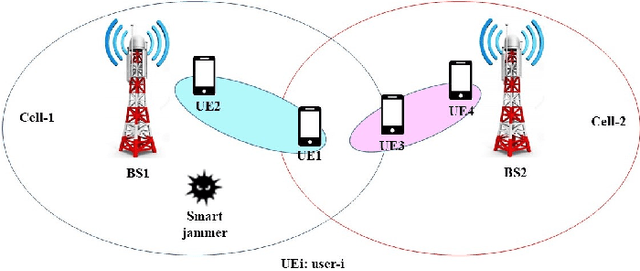
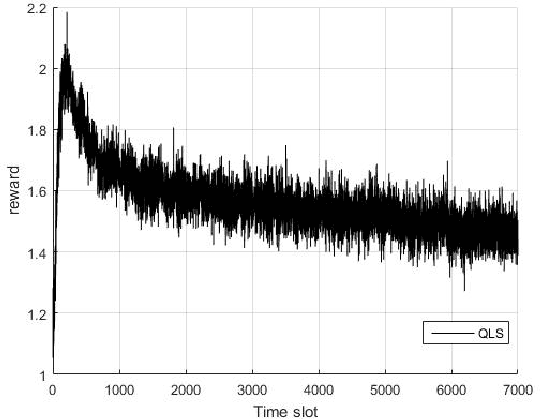
The performance of Non-orthogonal Multiple Access (NOMA) system dramatically decreases in the presence of inter-cell interference. This condition gets more challenging if a smart jammer is interacting in a network. In this paper, the NOMA power allocation of two independent Base Stations (BSs) against a smart jammer is, modeled as a sequential game. In this game, at first, each BS as a leader independently chooses its power allocation strategy. Then, the smart jammer as the follower selects its optimal strategy based on the strategies of the BSs. The solutions of this game are, derived under different conditions. Based on the game-theoretical analysis, three new schemes are proposed for anti-jamming NOMA power allocation in a two-cell scenario called a) Q-Learning based Unselfish (QLU) NOMA power allocation scheme, b) Deep Q-Learning based Unselfish (DQLU) NOMA power allocation scheme, and c) Hot Booting Deep Q-Learning based Unselfish (HBDQLU) NOMA power allocation scheme. In these methods the BSs do not coordinate with each other. But our analysis theoretically predicts that with high probability, the proposed methods will converge to the optimal strategy from the total network point of view. Simulation results show the convergence of the proposed schemes and also their outperformance with respect to the Q-Learning-based Selfish (QLS) NOMA power allocation method.

Deep Learning Approach for Matrix Completion Using Manifold Learning

Matrix completion has received vast amount of attention and research due to its wide applications in various study fields. Existing methods of matrix completion consider only nonlinear (or linear) relations among entries in a data matrix and ignore linear (or nonlinear) relationships latent. This paper introduces a new latent variables model for data matrix which is a combination of linear and nonlinear models and designs a novel deep-neural-network-based matrix completion algorithm to address both linear and nonlinear relations among entries of data matrix. The proposed method consists of two branches. The first branch learns the latent representations of columns and reconstructs the columns of the partially observed matrix through a series of hidden neural network layers. The second branch does the same for the rows. In addition, based on multi-task learning principles, we enforce these two branches work together and introduce a new regularization technique to reduce over-fitting. More specifically, the missing entries of data are recovered as a main task and manifold learning is performed as an auxiliary task. The auxiliary task constrains the weights of the network so it can be considered as a regularizer, improving the main task and reducing over-fitting. Experimental results obtained on the synthetic data and several real-world data verify the effectiveness of the proposed method compared with state-of-the-art matrix completion methods.