Low-Rank Isomap Algorithm
Paper and Code
Mar 06, 2021
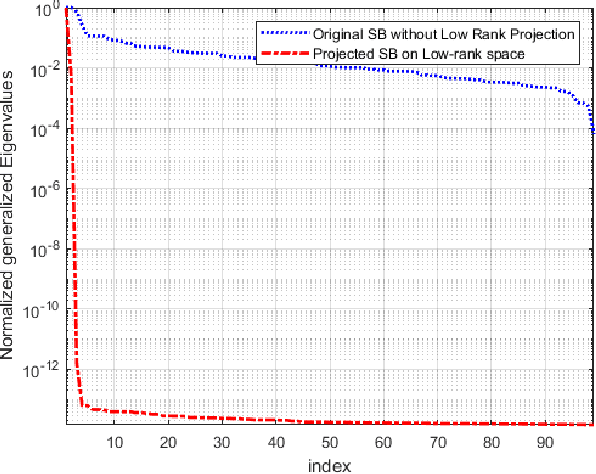
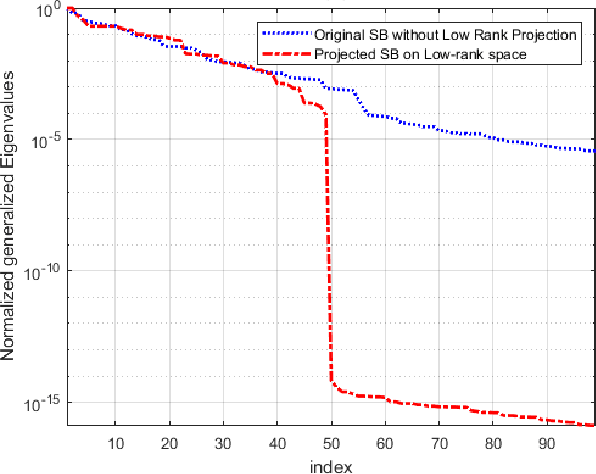
The Isomap is a well-known nonlinear dimensionality reduction method that highly suffers from computational complexity. Its computational complexity mainly arises from two stages; a) embedding a full graph on the data in the ambient space, and b) a complete eigenvalue decomposition. Although the reduction of the computational complexity of the graphing stage has been investigated, yet the eigenvalue decomposition stage remains a bottleneck in the problem. In this paper, we propose the Low-Rank Isomap algorithm by introducing a projection operator on the embedded graph from the ambient space to a low-rank latent space to facilitate applying the partial eigenvalue decomposition. This approach leads to reducing the complexity of Isomap to a linear order while preserving the structural information during the dimensionality reduction process. The superiority of the Low-Rank Isomap algorithm compared to some state-of-art algorithms is experimentally verified on facial image clustering in terms of speed and accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge