Task Allocation for Asynchronous Mobile Edge Learning with Delay and Energy Constraints

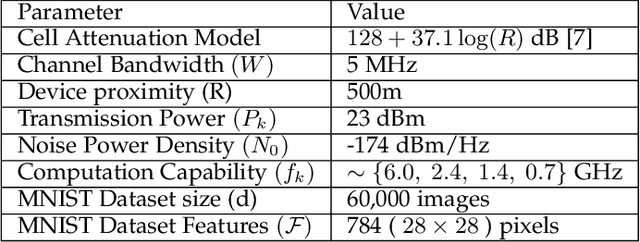
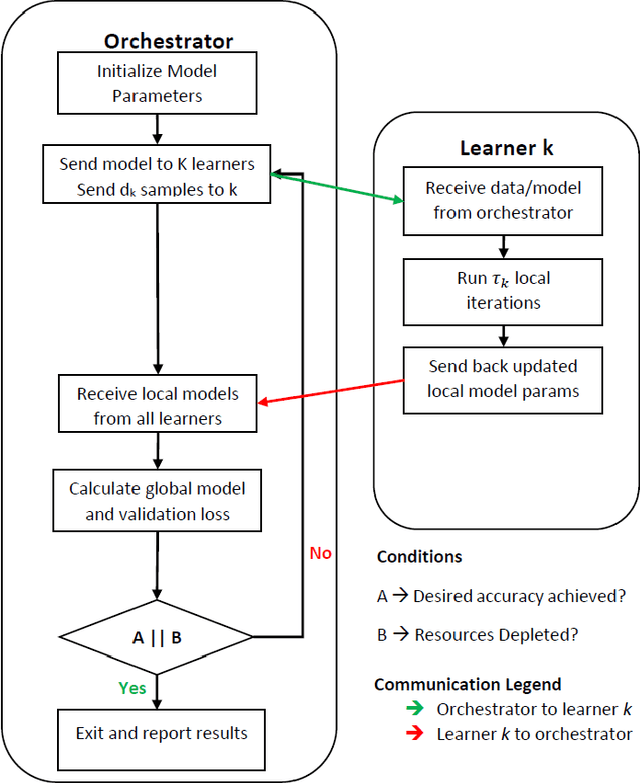
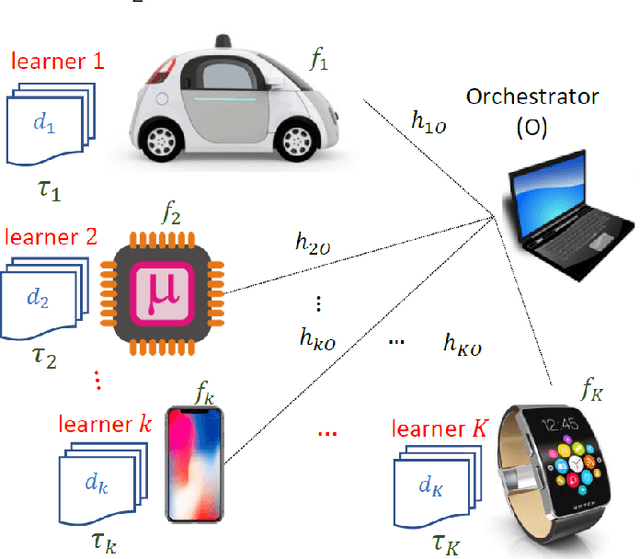
This paper extends the paradigm of "mobile edge learning (MEL)" by designing an optimal task allocation scheme for training a machine learning model in an asynchronous manner across mutiple edge nodes or learners connected via a resource-constrained wireless edge network. The optimization is done such that the portion of the task allotted to each learner is completed within a given global delay constraint and a local maximum energy consumption limit. The time and energy consumed are related directly to the heterogeneous communication and computational capabilities of the learners; i.e. the proposed model is heterogeneity aware (HA). Because the resulting optimization is an NP-hard quadratically-constrained integer linear program (QCILP), a two-step suggest-and-improve (SAI) solution is proposed based on using the solution of the relaxed synchronous problem to obtain the solution to the asynchronous problem. The proposed HA asynchronous (HA-Asyn) approach is compared against the HA synchronous (HA-Sync) scheme and the heterogeneity unaware (HU) equal batch allocation scheme. Results from a system of 20 learners tested for various completion time and energy consumption constraints show that the proposed HA-Asyn method works better than the HU synchronous/asynchronous (HU-Sync/Asyn) approach and can provide gains of up-to 25\% compared to the HA-Sync scheme.

Optimal Task Allocation for Mobile Edge Learning with Global Training Time Constraints

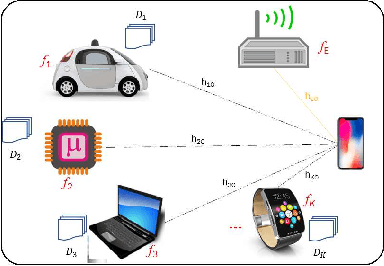
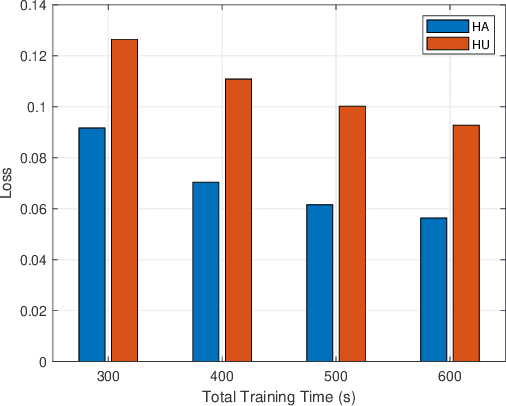
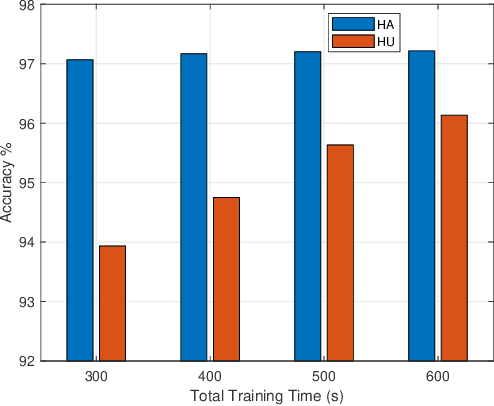
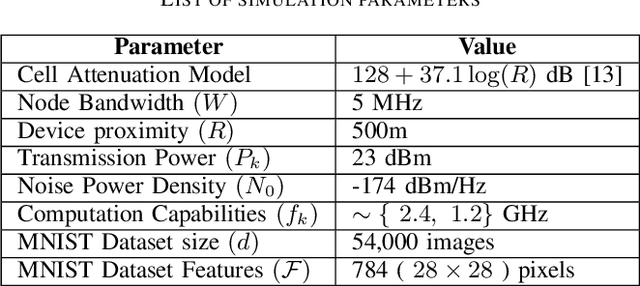
This paper proposes to minimize the loss of training a distributed machine learning (ML) model on nodes or learners connected via the resource-constrained wireless edge network by jointly optimizing the number of local and global updates and the task size allocation. The optimization is done while taking into account heterogeneous communication and computation capabilities of each learner. It is shown that the problem of interest cannot be solved analytically but by leveraging existing bounds on the difference between the optimal loss and the loss at any given iteration, an expression for the objective function is derived as a function of the number of local updates. It is shown that the problem is convex and can be solved by finding the argument that minimizes the loss. The result is then used to determine the batch sizes for each learner for the next global update step. The merits of the proposed solution, which is heterogeneity aware (HA), are exhibited by comparing its performance to the heterogeneity unaware (HU) approach.