Mithun P. Acharya
Neighborhood Structure Assisted Non-negative Matrix Factorization and its Application in Unsupervised Point Anomaly Detection
Jan 17, 2020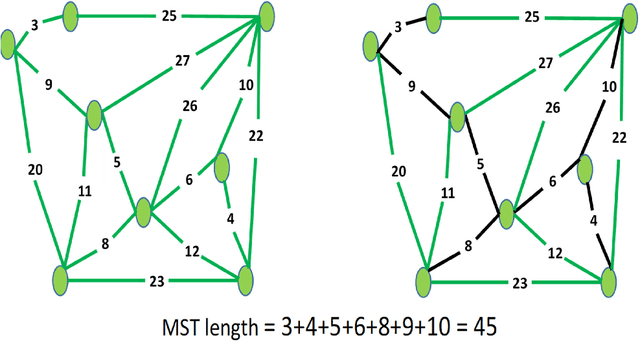
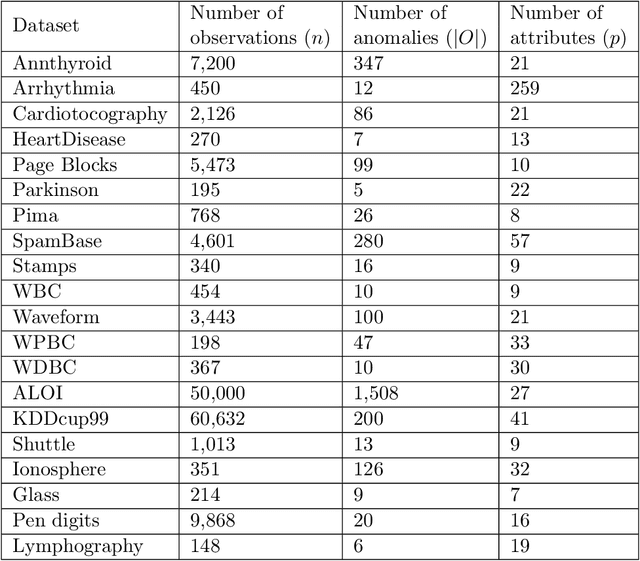
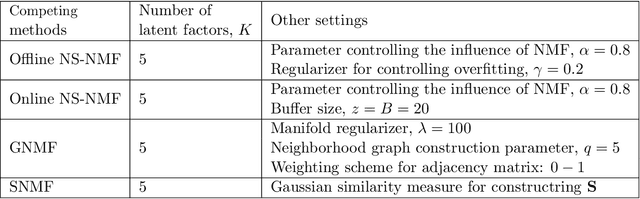
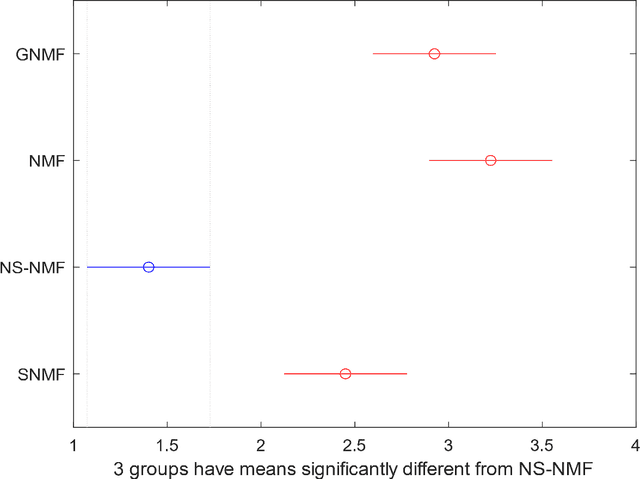
Abstract:Dimensionality reduction is considered as an important step for ensuring competitive performance in unsupervised learning such as anomaly detection. Non-negative matrix factorization (NMF) is a popular and widely used method to accomplish this goal. But NMF, together with its recent, enhanced version, like graph regularized NMF or symmetric NMF, do not have the provision to include the neighborhood structure information and, as a result, may fail to provide satisfactory performance in presence of nonlinear manifold structure. To address that shortcoming, we propose to consider and incorporate the neighborhood structural similarity information within the NMF framework by modeling the data through a minimum spanning tree. What motivates our choice is the understanding that in the presence of complicated data structure, a minimum spanning tree can approximate the intrinsic distance between two data points better than a simple Euclidean distance does, and consequently, it constitutes a more reasonable basis for differentiating anomalies from the normal class data. We label the resulting method as the neighborhood structure assisted NMF. By comparing the formulation and properties of the neighborhood structure assisted NMF with other versions of NMF including graph regularized NMF and symmetric NMF, it is apparent that the inclusion of the neighborhood structure information using minimum spanning tree makes a key difference. We further devise both offline and online algorithmic versions of the proposed method. Empirical comparisons using twenty benchmark datasets as well as an industrial dataset extracted from a hydropower plant demonstrate the superiority of the neighborhood structure assisted NMF and support our claim of merit.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge