Mithun Goutham
Epsilon-Neighborhood Decision-Boundary Governed Estimation (EDGE) of 2D Black Box Classifier Functions
Apr 13, 2025
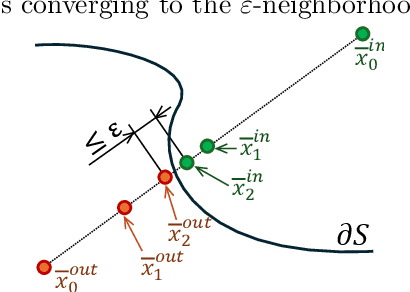


Abstract:Accurately estimating decision boundaries in black box systems is critical when ensuring safety, quality, and feasibility in real-world applications. However, existing methods iteratively refine boundary estimates by sampling in regions of uncertainty, without providing guarantees on the closeness to the decision boundary and also result in unnecessary exploration that is especially disadvantageous when evaluations are costly. This paper presents the Epsilon-Neighborhood Decision-Boundary Governed Estimation (EDGE), a sample efficient and function-agnostic algorithm that leverages the intermediate value theorem to estimate the location of the decision boundary of a black box binary classifier within a user-specified epsilon-neighborhood. Evaluations are conducted on three nonlinear test functions and a case study of an electric grid stability problem with uncertain renewable power injection. The EDGE algorithm demonstrates superior sample efficiency and better boundary approximation than adaptive sampling techniques and grid-based searches.
Resilient Fleet Management for Energy-Aware Intra-Factory Logistics
Mar 16, 2024Abstract:This paper presents a novel fleet management strategy for battery-powered robot fleets tasked with intra-factory logistics in an autonomous manufacturing facility. In this environment, repetitive material handling operations are subject to real-world uncertainties such as blocked passages, and equipment or robot malfunctions. In such cases, centralized approaches enhance resilience by immediately adjusting the task allocation between the robots. To overcome the computational expense, a two-step methodology is proposed where the nominal problem is solved a priori using a Monte Carlo Tree Search algorithm for task allocation, resulting in a nominal search tree. When a disruption occurs, the nominal search tree is rapidly updated a posteriori with costs to the new problem while simultaneously generating feasible solutions. Computational experiments prove the real-time capability of the proposed algorithm for various scenarios and compare it with the case where the search tree is not used and the decentralized approach that does not attempt task reassignment.
Greedy Heuristics Adapted for the Multi-commodity Pickup and Delivery Traveling Salesman Problem
Mar 09, 2023Abstract:The Multi-Commodity One-to-One Pickup and Delivery Traveling Salesman Problem finds the optimal tour that transports a set of unique commodities from their pickup to delivery locations, while never exceeding the maximum payload capacity of the material handling agent. For this NP hard problem, this paper presents adaptations of the nearest neighbor and cheapest insertion heuristics to account for the constraints related to the precedence between the locations and the cargo capacity limitations. To test the effectiveness of the proposed algorithms, the well-known TSPLIB benchmark data-set is modified in a replicable manner to create precedence constraints, while varying the cargo capacity of the agent. It is seen that the adapted Nearest Neighbor heuristic outperforms the adapted Cheapest Insertion algorithm in the majority of the cases studied, while providing near instantaneous solutions.
A Convex Hull Cheapest Insertion Heuristic for the Non-Euclidean and Precedence Constrained TSPs
Feb 05, 2023Abstract:The convex hull cheapest insertion heuristic is known to generate good solutions to the Euclidean Traveling Salesperson Problem. This paper presents an adaptation of this heuristic to the non-Euclidean version of the problem and further extends it to the problem with precedence constraints, also known as the Sequential Ordering Problem. To test the proposed algorithm, the well-known TSPLIB benchmark data-set is modified in a replicable manner to create non-Euclidean instances and precedence constraints. The proposed algorithm is shown to outperform the commonly used Nearest Neighbor algorithm in 97% of the cases that do not have precedence constraints. When precedence constraints exist such that the child nodes are centrally located, the algorithm again outperforms the Nearest Neighbor algorithm in 98% of the studied instances. Considering all spatial layouts of precedence constraints, the algorithm outperforms the Nearest Neighbor heuristic 68% of the time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge