Hierarchically Consistent Motion Primitives for Quadrotor Coordination

We present a hierarchical framework for motion planning of a large collection of agents. The proposed framework starts from low level motion primitives over a gridded workspace and provides a set of rules for constructing higher level motion primitives. Our hierarchical approach is highly scalable and robust making it an ideal tool for planning for multi-agent systems. Results are demonstrated experimentally on a collection of quadrotors that must navigate a cluttered environment while maintaining a formation.

A Modular Framework for Motion Planning using Safe-by-Design Motion Primitives

We present a modular framework for solving a motion planning problem among a group of robots. The proposed framework utilizes a finite set of low level motion primitives to generate motions in a gridded workspace. The constraints on allowable sequences of motion primitives are formalized through a maneuver automaton. At the high level, a control policy determines which motion primitive is executed in each box of the gridded workspace. We state general conditions on motion primitives to obtain provably correct behavior so that a library of safe-by-design motion primitives can be designed. The overall framework yields a highly robust design by utilizing feedback strategies at both the low and high levels. We provide specific designs for motion primitives and control policies suitable for multi-robot motion planning; the modularity of our approach enables one to independently customize the designs of each of these components. Our approach is experimentally validated on a group of quadrocopters.

Safe and Robust Robot Maneuvers Based on Reach Control

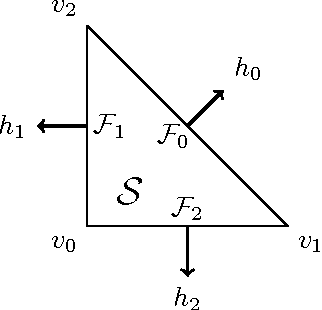
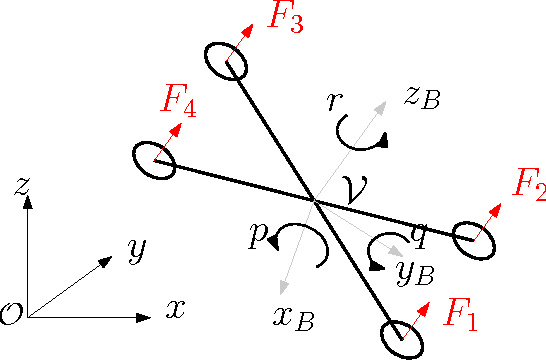
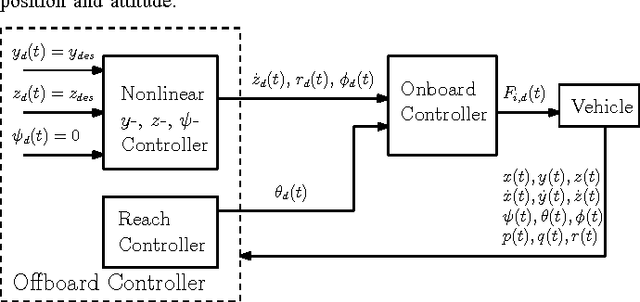
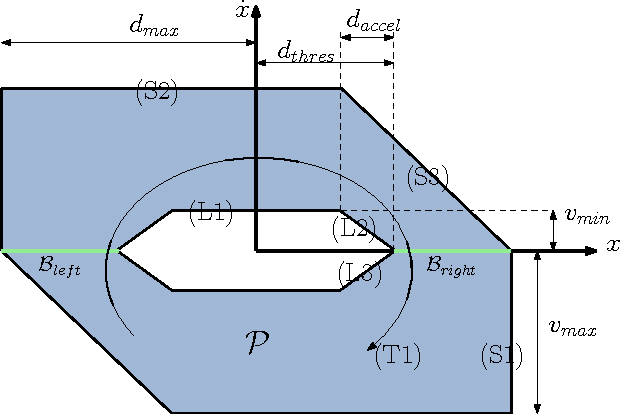
In this paper, we investigate the synthesis of piecewise affine feedback controllers to address the problem of safe and robust controller design in robotics based on high-level controls specifications. The methodology is based on formulating the problem as a collection of reach control problems on a polytopic state space. Reach control has so far only been developed in theory and has not been tested experimentally on a real system before. Using a quadrocopter as our experimental platform, we show that these theoretical tools can achieve fast, albeit safe and robust maneuvers. In contrast to most traditional control techniques, the reach control approach does not require a predefined open-loop reference trajectory or spacial path. Experimental results on a quadrocopter show the effectiveness and robustness of this control approach. In a proof-of-concept demonstration, the reach controller is implemented in one translational direction while the other degrees of freedom are stabilized by separate controllers.

Curve Shortening and the Rendezvous Problem for Mobile Autonomous Robots

If a smooth, closed, and embedded curve is deformed along its normal vector field at a rate proportional to its curvature, it shrinks to a circular point. This curve evolution is called Euclidean curve shortening and the result is known as the Gage-Hamilton-Grayson Theorem. Motivated by the rendezvous problem for mobile autonomous robots, we address the problem of creating a polygon shortening flow. A linear scheme is proposed that exhibits several analogues to Euclidean curve shortening: The polygon shrinks to an elliptical point, convex polygons remain convex, and the perimeter of the polygon is monotonically decreasing.