Mingye Song
Fast Randomized PCA for Sparse Data
Oct 16, 2018
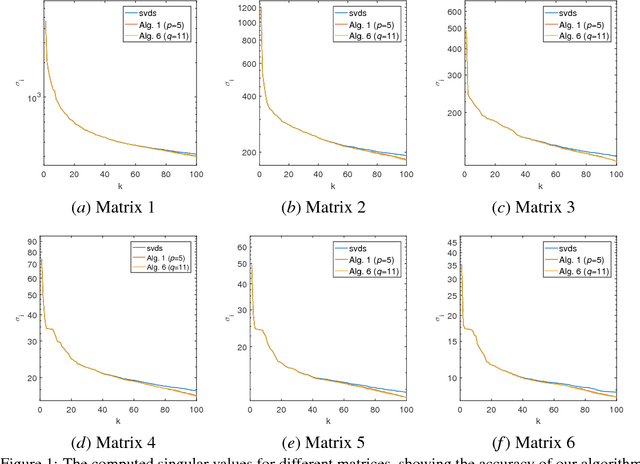

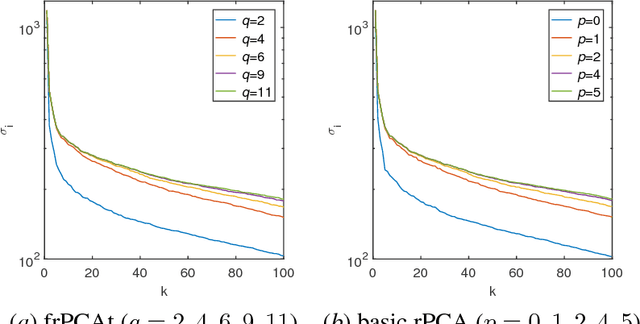
Abstract:Principal component analysis (PCA) is widely used for dimension reduction and embedding of real data in social network analysis, information retrieval, and natural language processing, etc. In this work we propose a fast randomized PCA algorithm for processing large sparse data. The algorithm has similar accuracy to the basic randomized SVD (rPCA) algorithm (Halko et al., 2011), but is largely optimized for sparse data. It also has good flexibility to trade off runtime against accuracy for practical usage. Experiments on real data show that the proposed algorithm is up to 9.1X faster than the basic rPCA algorithm without accuracy loss, and is up to 20X faster than the svds in Matlab with little error. The algorithm computes the first 100 principal components of a large information retrieval data with 12,869,521 persons and 323,899 keywords in less than 400 seconds on a 24-core machine, while all conventional methods fail due to the out-of-memory issue.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge