Provable learning of quantum states with graphical models

The complete learning of an $n$-qubit quantum state requires samples exponentially in $n$. Several works consider subclasses of quantum states that can be learned in polynomial sample complexity such as stabilizer states or high-temperature Gibbs states. Other works consider a weaker sense of learning, such as PAC learning and shadow tomography. In this work, we consider learning states that are close to neural network quantum states, which can efficiently be represented by a graphical model called restricted Boltzmann machines (RBMs). To this end, we exhibit robustness results for efficient provable two-hop neighborhood learning algorithms for ferromagnetic and locally consistent RBMs. We consider the $L_p$-norm as a measure of closeness, including both total variation distance and max-norm distance in the limit. Our results allow certain quantum states to be learned with a sample complexity \textit{exponentially} better than naive tomography. We hence provide new classes of efficiently learnable quantum states and apply new strategies to learn them.

Negative Shannon Information Hides Networks

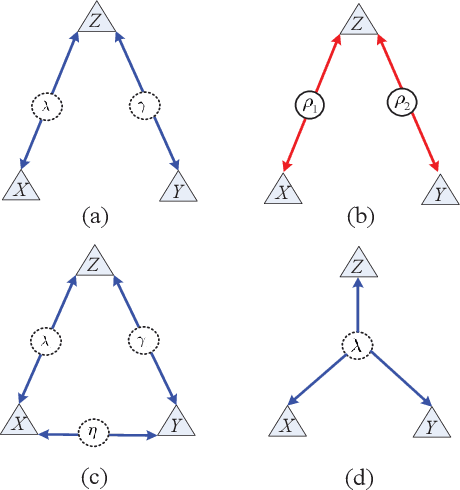
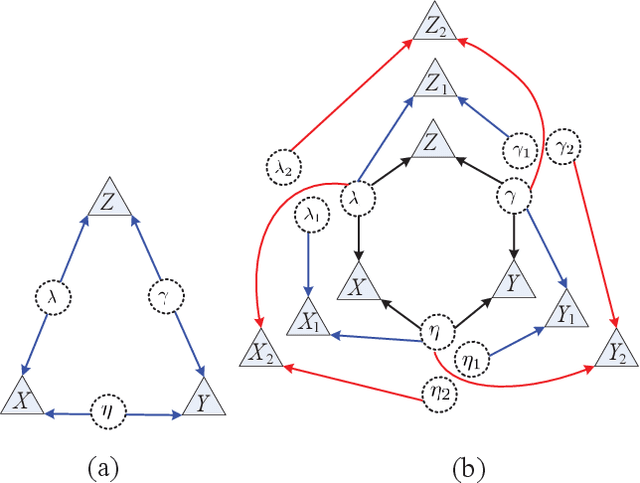
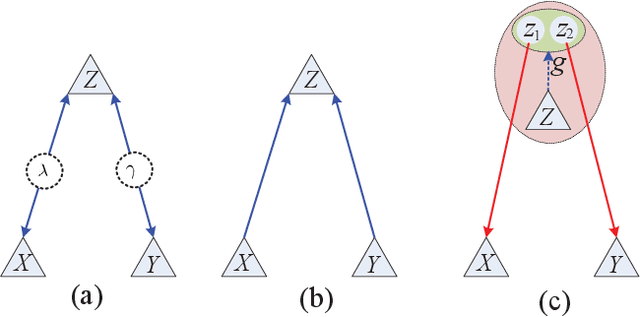
Negative numbers are essential in mathematics. They are not needed to describe statistical experiments, as those are expressed in terms of positive probabilities. Shannon information was firstly defined for characterizing informational uncertainty of classical probabilistic distributions. However, it is unknown why there is negative information for more than two random variables on finite sample spaces. We first show the negative Shannon mutual information of three random variables implies Bayesian network representations of its joint distribution. We then show the intrinsic compatibility with negative Shannon information is generic for Bayesian networks with quantum realizations. This further suggests a new kind of space-dependent nonlocality. The present result provides a device-independent witness of negative Shannon information.