Negative Shannon Information Hides Networks
Paper and Code
Jun 09, 2022
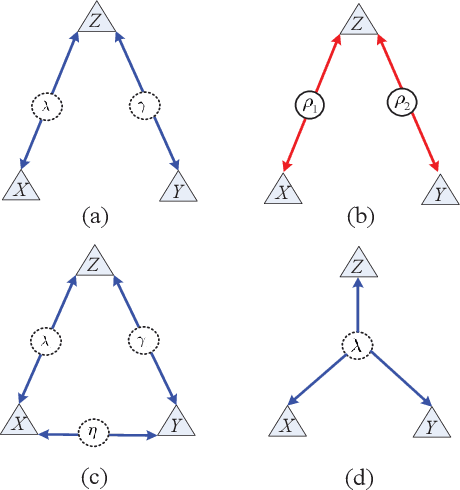
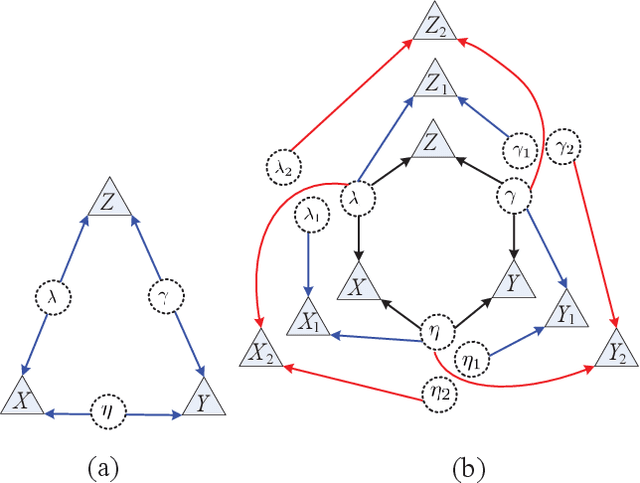
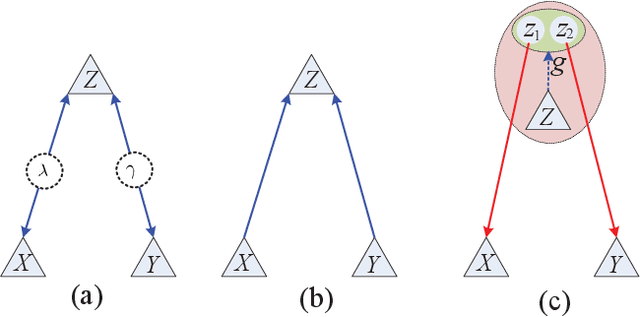
Negative numbers are essential in mathematics. They are not needed to describe statistical experiments, as those are expressed in terms of positive probabilities. Shannon information was firstly defined for characterizing informational uncertainty of classical probabilistic distributions. However, it is unknown why there is negative information for more than two random variables on finite sample spaces. We first show the negative Shannon mutual information of three random variables implies Bayesian network representations of its joint distribution. We then show the intrinsic compatibility with negative Shannon information is generic for Bayesian networks with quantum realizations. This further suggests a new kind of space-dependent nonlocality. The present result provides a device-independent witness of negative Shannon information.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge