Exponential tail bounds and Large Deviation Principle for Heavy-Tailed U-Statistics

We study deviation of U-statistics when samples have heavy-tailed distribution so the kernel of the U-statistic does not have bounded exponential moments at any positive point. We obtain an exponential upper bound for the tail of the U-statistics which clearly denotes two regions of tail decay, the first is a Gaussian decay and the second behaves like the tail of the kernel. For several common U-statistics, we also show the upper bound has the right rate of decay as well as sharp constants by obtaining rough logarithmic limits which in turn can be used to develop LDP for U-statistics. In spite of usual LDP results in the literature, processes we consider in this work have LDP speed slower than their sample size $n$.

A practical algorithm to calculate Cap Discrepancy

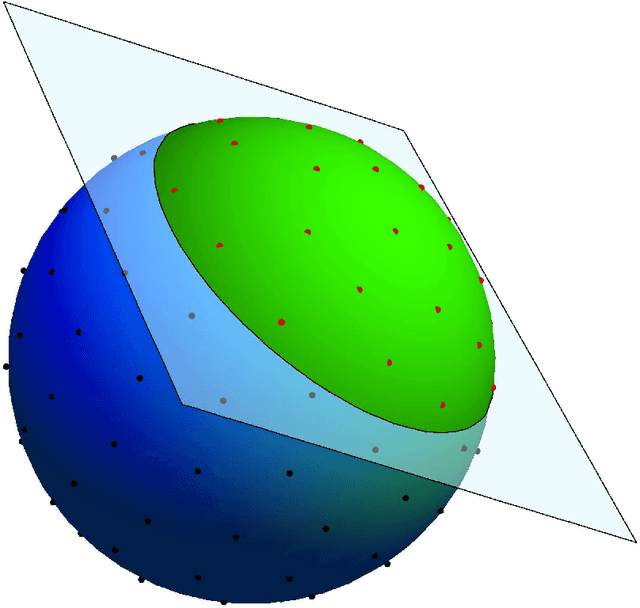
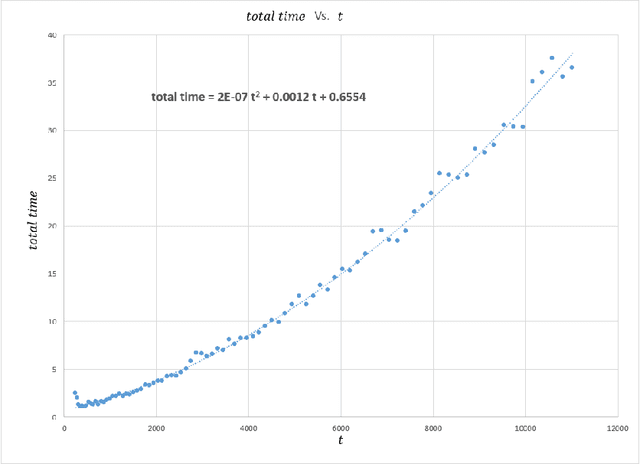
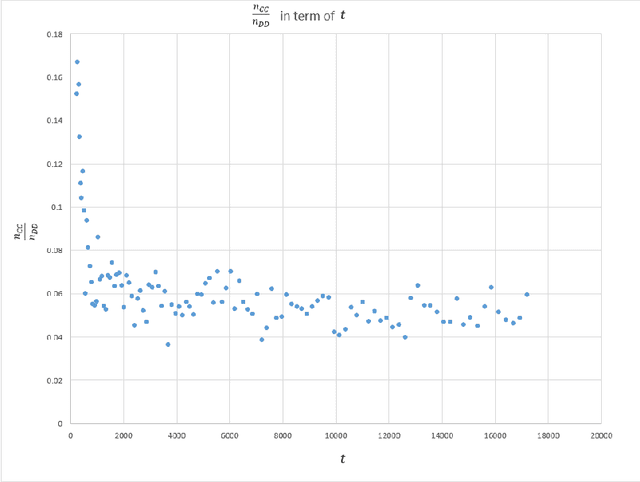
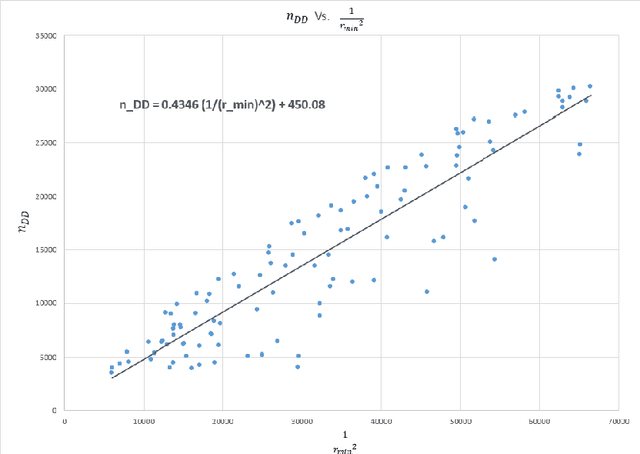
Uniform distribution of the points has been of interest to researchers for a long time and has applications in different areas of Mathematics and Computer Science. One of the well-known measures to evaluate the uniformity of a given distribution is Discrepancy, which assesses the difference between the Uniform distribution and the empirical distribution given by putting mass points at the points of the given set. While Discrepancy is very useful to measure uniformity, it is computationally challenging to be calculated accurately. We introduce the concept of directed Discrepancy based on which we have developed an algorithm, called Directional Discrepancy, that can offer accurate approximation for the cap Discrepancy of a finite set distributed on the unit Sphere, $\mathbb{S}^2.$ We also analyze the time complexity of the Directional Discrepancy algorithm precisely; and practically evaluate its capacity by calculating the Cap Discrepancy of a specific distribution, Polar Coordinates, which aims to distribute points uniformly on the Sphere.

Sharp Concentration Results for Heavy-Tailed Distributions

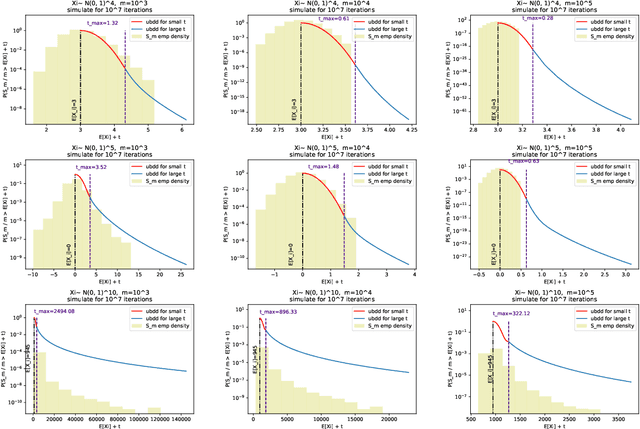
We obtain concentration and large deviation for the sums of independent and identically distributed random variables with heavy-tailed distributions. Our concentration results are concerned with random variables whose distributions satisfy $P(X>t) \leq {\rm e}^{- I(t)}$, where $I: \mathbb{R} \rightarrow \mathbb{R}$ is an increasing function and $I(t)/t \rightarrow \alpha \in [0, \infty)$ as $t \rightarrow \infty$. Our main theorem can not only recover some of the existing results, such as the concentration of the sum of subWeibull random variables, but it can also produce new results for the sum of random variables with heavier tails. We show that the concentration inequalities we obtain are sharp enough to offer large deviation results for the sums of independent random variables as well. Our analyses which are based on standard truncation arguments simplify, unify and generalize the existing results on the concentration and large deviation of heavy-tailed random variables.