Ali Kamalinejad
A practical algorithm to calculate Cap Discrepancy
Oct 20, 2020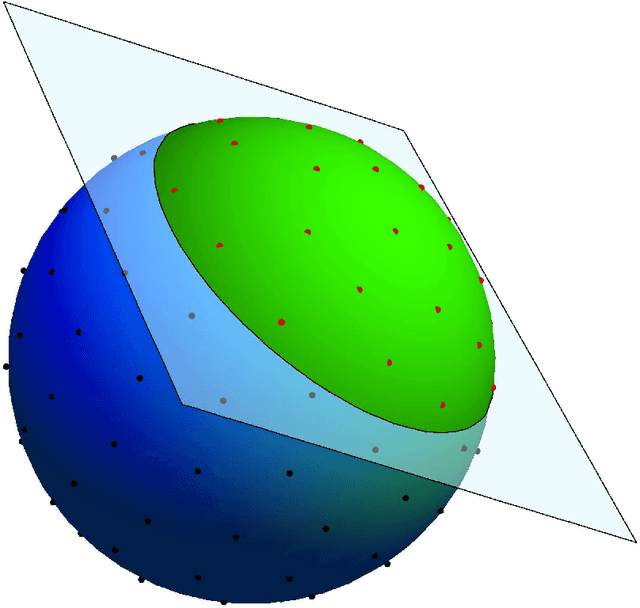
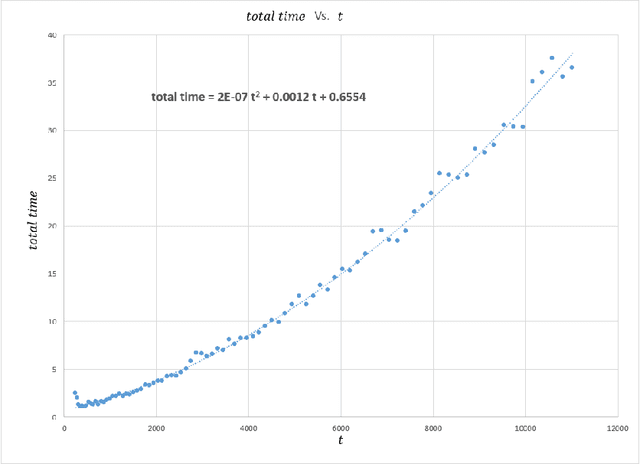
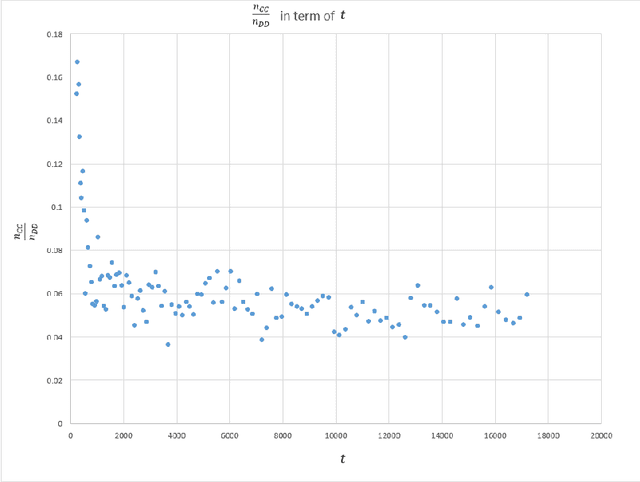
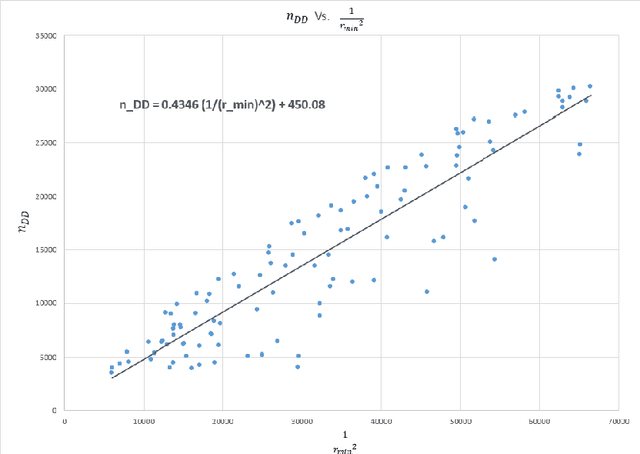
Abstract:Uniform distribution of the points has been of interest to researchers for a long time and has applications in different areas of Mathematics and Computer Science. One of the well-known measures to evaluate the uniformity of a given distribution is Discrepancy, which assesses the difference between the Uniform distribution and the empirical distribution given by putting mass points at the points of the given set. While Discrepancy is very useful to measure uniformity, it is computationally challenging to be calculated accurately. We introduce the concept of directed Discrepancy based on which we have developed an algorithm, called Directional Discrepancy, that can offer accurate approximation for the cap Discrepancy of a finite set distributed on the unit Sphere, $\mathbb{S}^2.$ We also analyze the time complexity of the Directional Discrepancy algorithm precisely; and practically evaluate its capacity by calculating the Cap Discrepancy of a specific distribution, Polar Coordinates, which aims to distribute points uniformly on the Sphere.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge