Mike Giles
Multilevel Monte Carlo for Scalable Bayesian Computations
Sep 15, 2016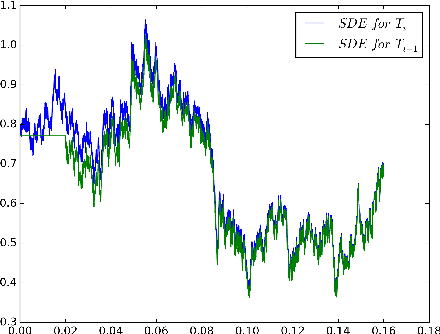
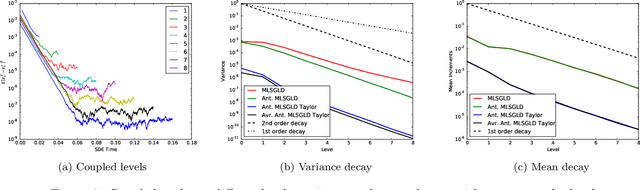
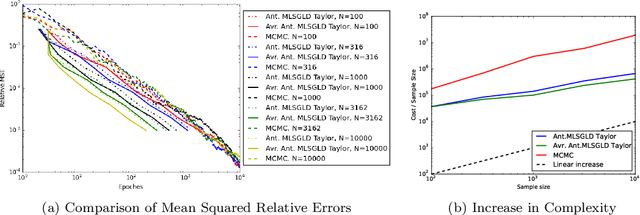
Abstract:Markov chain Monte Carlo (MCMC) algorithms are ubiquitous in Bayesian computations. However, they need to access the full data set in order to evaluate the posterior density at every step of the algorithm. This results in a great computational burden in big data applications. In contrast to MCMC methods, Stochastic Gradient MCMC (SGMCMC) algorithms such as the Stochastic Gradient Langevin Dynamics (SGLD) only require access to a batch of the data set at every step. This drastically improves the computational performance and scales well to large data sets. However, the difficulty with SGMCMC algorithms comes from the sensitivity to its parameters which are notoriously difficult to tune. Moreover, the Root Mean Square Error (RMSE) scales as $\mathcal{O}(c^{-\frac{1}{3}})$ as opposed to standard MCMC $\mathcal{O}(c^{-\frac{1}{2}})$ where $c$ is the computational cost. We introduce a new class of Multilevel Stochastic Gradient Markov chain Monte Carlo algorithms that are able to mitigate the problem of tuning the step size and more importantly of recovering the $\mathcal{O}(c^{-\frac{1}{2}})$ convergence of standard Markov Chain Monte Carlo methods without the need to introduce Metropolis-Hasting steps. A further advantage of this new class of algorithms is that it can easily be parallelised over a heterogeneous computer architecture. We illustrate our methodology using Bayesian logistic regression and provide numerical evidence that for a prescribed relative RMSE the computational cost is sublinear in the number of data items.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge