Conditional Neural Processes for Molecules

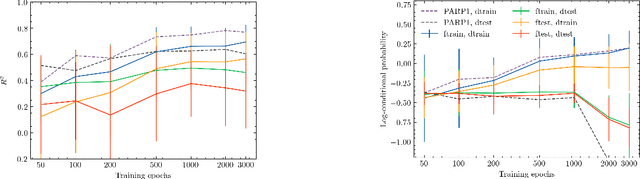
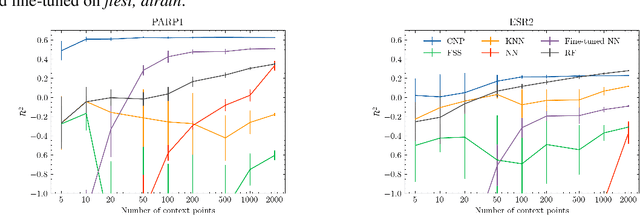
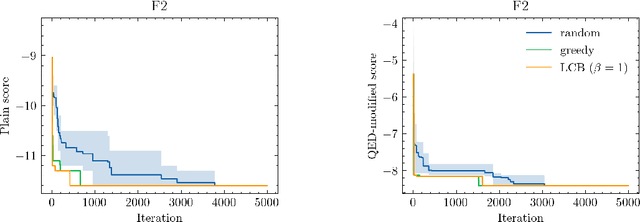
Neural processes (NPs) are models for transfer learning with properties reminiscent of Gaussian Processes (GPs). They are adept at modelling data consisting of few observations of many related functions on the same input space and are trained by minimizing a variational objective, which is computationally much less expensive than the Bayesian updating required by GPs. So far, most studies of NPs have focused on low-dimensional datasets which are not representative of realistic transfer learning tasks. Drug discovery is one application area that is characterized by datasets consisting of many chemical properties or functions which are sparsely observed, yet depend on shared features or representations of the molecular inputs. This paper applies the conditional neural process (CNP) to DOCKSTRING, a dataset of docking scores for benchmarking ML models. CNPs show competitive performance in few-shot learning tasks relative to supervised learning baselines common in QSAR modelling, as well as an alternative model for transfer learning based on pre-training and refining neural network regressors. We present a Bayesian optimization experiment which showcases the probabilistic nature of CNPs and discuss shortcomings of the model in uncertainty quantification.

Achieving Robustness to Aleatoric Uncertainty with Heteroscedastic Bayesian Optimisation

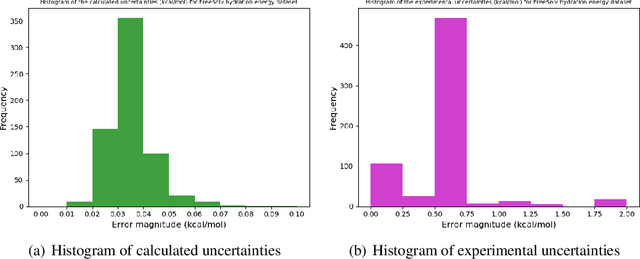
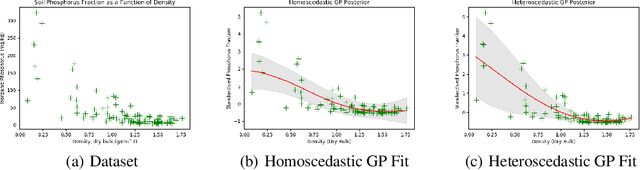
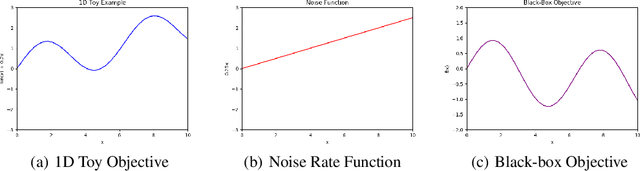
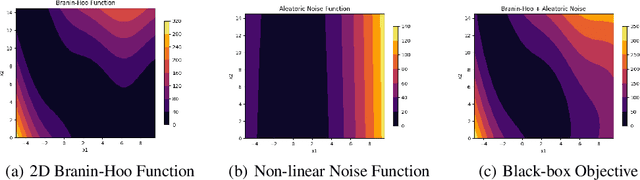
Bayesian optimisation is an important decision-making tool for high-stakes applications in drug discovery and materials design. An oft-overlooked modelling consideration however is the representation of input-dependent or heteroscedastic aleatoric uncertainty. The cost of misrepresenting this uncertainty as being homoscedastic could be high in drug discovery applications where neglecting heteroscedasticity in high throughput virtual screening could lead to a failed drug discovery program. In this paper, we propose a heteroscedastic Bayesian optimisation scheme which both represents and penalises aleatoric noise in the suggestions.Our scheme features a heteroscedastic Gaussian Process (GP) as the surrogate model in conjunction with two acquisition heuristics. First, we extend the augmented expected improvement (AEI) heuristic to the heteroscedastic setting and second, we introduce a new acquisition function, aleatoric-penalised expected improvement (ANPEI) based on a simple scalarisation of the performance and noise objective. Both methods penalise aleatoric noise in the suggestions and yield improved performance relative to a naive implementation of homoscedastic Bayesian optimisation on toy problems as well as a real-world optimisation problem.