$\varepsilon$-fractional Core Stability in Hedonic Games

Hedonic Games (HGs) are a classical framework modeling coalition formation of strategic agents guided by their individual preferences. According to these preferences, it is desirable that a coalition structure (i.e. a partition of agents into coalitions) satisfies some form of stability. The most well-known and natural of such notions is arguably core-stability. Informally, a partition is core-stable if no subset of agents would like to deviate by regrouping in a so-called core-blocking coalition. Unfortunately, core-stable partitions seldom exist and even when they do, it is often computationally intractable to find one. To circumvent these problems, we propose the notion of $\varepsilon$-fractional core-stability, where at most an $\varepsilon$-fraction of all possible coalitions is allowed to core-block. It turns out that such a relaxation may guarantee both existence and polynomial-time computation. Specifically, we design efficient algorithms returning an $\varepsilon$-fractional core-stable partition, with $\varepsilon$ exponentially decreasing in the number of agents, for two fundamental classes of HGs: Simple Fractional and Anonymous. From a probabilistic point of view, being the definition of $\varepsilon$-fractional core equivalent to requiring that uniformly sampled coalitions core-block with probability lower than $\varepsilon$, we further extend the definition to handle more complex sampling distributions. Along this line, when valuations have to be learned from samples in a PAC-learning fashion, we give positive and negative results on which distributions allow the efficient computation of outcomes that are $\varepsilon$-fractional core-stable with arbitrarily high confidence.

PAC learning and stabilizing Hedonic Games: towards a unifying approach

We study PAC learnability and PAC stabilizability of Hedonic Games (HGs), i.e., efficiently inferring preferences or core-stable partitions from samples. We first expand the known learnability/stabilizability landscape for some of the most prominent HGs classes, providing results for Friends and Enemies Games, Bottom Responsive, and Anonymous HGs. Then, having a broader view in mind, we attempt to shed light on the structural properties leading to learnability/stabilizability, or lack thereof, for specific HGs classes. Along this path, we focus on the fully expressive Hedonic Coalition Nets representation of HGs. We identify two sets of conditions that lead to efficient learnability, and which encompass all of the known positive learnability results. On the side of stability, we reveal that, while the freedom of choosing an ad hoc adversarial distribution is the most obvious hurdle to achieving PAC stability, it is not the only one. First, we show a distribution independent necessary condition for PAC stability. Then, we focus on $\W$-games, where players have individual preferences over other players and evaluate coalitions based on the least preferred member. We prove that these games are PAC stabilizable under the class of bounded distributions, which assign positive probability mass to all coalitions. Finally, we discuss why such a result is not easily extendable to other HGs classes even in this promising scenario. Namely, we establish a purely computational property necessary for achieving PAC stability.

Unavailable Transit Feed Specification: Making it Available with Recurrent Neural Networks

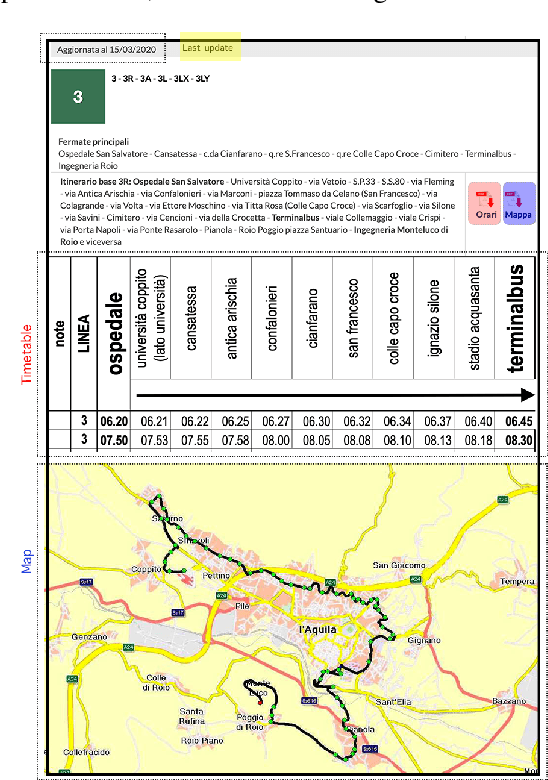
Studies on public transportation in Europe suggest that European inhabitants use buses in ca. 56% of all public transport travels. One of the critical factors affecting such a percentage and more, in general, the demand for public transport services, with an increasing reluctance to use them, is their quality. End-users can perceive quality from various perspectives, including the availability of information, i.e., the access to details about the transit and the provided services. The approach proposed in this paper, using innovative methodologies resorting on data mining and machine learning techniques, aims to make available the unavailable data about public transport. In particular, by mining GPS traces, we manage to reconstruct the complete transit graph of public transport. The approach has been successfully validated on a real dataset collected from the local bus system of the city of L'Aquila (Italy). The experimental results demonstrate that the proposed approach and implemented framework are both effective and efficient, thus being ready for deployment.

Strategyproof Mechanisms for Additively Separable Hedonic Games and Fractional Hedonic Games

Additively separable hedonic games and fractional hedonic games have received considerable attention. They are coalition forming games of selfish agents based on their mutual preferences. Most of the work in the literature characterizes the existence and structure of stable outcomes (i.e., partitions in coalitions), assuming that preferences are given. However, there is little discussion on this assumption. In fact, agents receive different utilities if they belong to different partitions, and thus it is natural for them to declare their preferences strategically in order to maximize their benefit. In this paper we consider strategyproof mechanisms for additively separable hedonic games and fractional hedonic games, that is, partitioning methods without payments such that utility maximizing agents have no incentive to lie about their true preferences. We focus on social welfare maximization and provide several lower and upper bounds on the performance achievable by strategyproof mechanisms for general and specific additive functions. In most of the cases we provide tight or asymptotically tight results. All our mechanisms are simple and can be computed in polynomial time. Moreover, all the lower bounds are unconditional, that is, they do not rely on any computational or complexity assumptions.