Impact of Single Rotations and Entanglement Topologies in Quantum Neural Networks

In this work, an analysis of the performance of different Variational Quantum Circuits is presented, investigating how it changes with respect to entanglement topology, adopted gates, and Quantum Machine Learning tasks to be performed. The objective of the analysis is to identify the optimal way to construct circuits for Quantum Neural Networks. In the presented experiments, two types of circuits are used: one with alternating layers of rotations and entanglement, and the other, similar to the first one, but with an additional final layer of rotations. As rotation layers, all combinations of one and two rotation sequences are considered. Four different entanglement topologies are compared: linear, circular, pairwise, and full. Different tasks are considered, namely the generation of probability distributions and images, and image classification. Achieved results are correlated with the expressibility and entanglement capability of the different circuits to understand how these features affect performance.

Triplet Loss Based Quantum Encoding for Class Separability

An efficient and data-driven encoding scheme is proposed to enhance the performance of variational quantum classifiers. This encoding is specially designed for complex datasets like images and seeks to help the classification task by producing input states that form well-separated clusters in the Hilbert space according to their classification labels. The encoding circuit is trained using a triplet loss function inspired by classical facial recognition algorithms, and class separability is measured via average trace distances between the encoded density matrices. Benchmark tests performed on various binary classification tasks on MNIST and MedMNIST datasets demonstrate considerable improvement over amplitude encoding with the same VQC structure while requiring a much lower circuit depth.

Training Variational Quantum Circuits Using Particle Swarm Optimization

In this work, the Particle Swarm Optimization (PSO) algorithm has been used to train various Variational Quantum Circuits (VQCs). This approach is motivated by the fact that commonly used gradient-based optimization methods can suffer from the barren plateaus problem. PSO is a stochastic optimization technique inspired by the collective behavior of a swarm of birds. The dimension of the swarm, the number of iterations of the algorithm, and the number of trainable parameters can be set. In this study, PSO has been used to train the entire structure of VQCs, allowing it to select which quantum gates to apply, the target qubits, and the rotation angle, in case a rotation is chosen. The algorithm is restricted to choosing from four types of gates: Rx, Ry, Rz, and CNOT. The proposed optimization approach has been tested on various datasets of the MedMNIST, which is a collection of biomedical image datasets designed for image classification tasks. Performance has been compared with the results achieved by classical stochastic gradient descent applied to a predefined VQC. The results show that the PSO can achieve comparable or even better classification accuracy across multiple datasets, despite the PSO using a lower number of quantum gates than the VQC used with gradient descent optimization.

SRBB-Based Quantum State Preparation

In this work, a scalable algorithm for the approximate quantum state preparation problem is proposed, facing a challenge of fundamental importance in many topic areas of quantum computing. The algorithm uses a variational quantum circuit based on the Standard Recursive Block Basis (SRBB), a hierarchical construction for the matrix algebra of the $SU(2^n)$ group, which is capable of linking the variational parameters with the topology of the Lie group. Compared to the full algebra, using only diagonal components reduces the number of CNOTs by an exponential factor, as well as the circuit depth, in full agreement with the relaxation principle, inherent to the approximation methodology, of minimizing resources while achieving high accuracy. The desired quantum state is then approximated by a scalable quantum neural network, which is designed upon the diagonal SRBB sub-algebra. This approach provides a new scheme for approximate quantum state preparation in a variational framework and a specific use case for the SRBB hierarchy. The performance of the algorithm is assessed with different loss functions, like fidelity, trace distance, and Frobenius norm, in relation to two optimizers: Adam and Nelder-Mead. The results highlight the potential of SRBB in close connection with the geometry of unitary groups, achieving high accuracy up to 4 qubits in simulation, but also its current limitations with an increasing number of qubits. Additionally, the approximate SRBB-based QSP algorithm has been tested on real quantum devices to assess its performance with a small number of qubits.

A Scalable Quantum Neural Network for Approximate SRBB-Based Unitary Synthesis

In this work, scalable quantum neural networks are introduced to approximate unitary evolutions through the Standard Recursive Block Basis (SRBB) and, subsequently, redesigned with a reduced number of CNOTs. This algebraic approach to the problem of unitary synthesis exploits Lie algebras and their topological features to obtain scalable parameterizations of unitary operators. First, the recursive algorithm that builds the SRBB is presented, framed in the original scalability scheme already known to the literature only from a theoretical point of view. Unexpectedly, 2-qubit systems emerge as a special case outside this scheme. Furthermore, an algorithm to reduce the number of CNOTs is proposed, thus deriving a new implementable scaling scheme that requires one single layer of approximation. From the mathematical algorithm, the scalable CNOT-reduced quantum neural network is implemented and its performance is assessed with a variety of different unitary matrices, both sparse and dense, up to 6 qubits via the PennyLane library. The effectiveness of the approximation is measured with different metrics in relation to two optimizers: a gradient-based method and the Nelder-Mead method. The approximate SRBB-based synthesis algorithm with CNOT-reduction is also tested on real hardware and compared with other valid approximation and decomposition methods available in the literature.

Multi-Class Quantum Convolutional Neural Networks

Classification is particularly relevant to Information Retrieval, as it is used in various subtasks of the search pipeline. In this work, we propose a quantum convolutional neural network (QCNN) for multi-class classification of classical data. The model is implemented using PennyLane. The optimization process is conducted by minimizing the cross-entropy loss through parameterized quantum circuit optimization. The QCNN is tested on the MNIST dataset with 4, 6, 8 and 10 classes. The results show that with 4 classes, the performance is slightly lower compared to the classical CNN, while with a higher number of classes, the QCNN outperforms the classical neural network.

Demonstration of Envariance and Parity Learning on the IBM 16 Qubit Processor

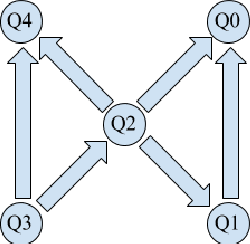
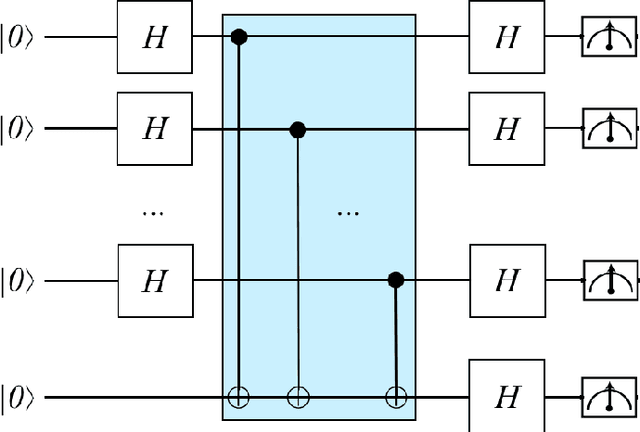
Recently, IBM has made available a quantum computer provided with 16 qubits, denoted as IBM Q16. Previously, only a 5 qubit device, denoted as Q5, was available. Both IBM devices can be used to run quantum programs, by means of a cloud-based platform. In this paper, we illustrate our experience with IBM Q16 in demonstrating entanglement assisted invariance, also known as envariance, and parity learning by querying a uniform quantum example oracle. In particular, we illustrate the non-trivial strategy we have designed for compiling $n$-qubit quantum circuits ($n$ being an input parameter) on any IBM device, taking into account topological constraints.

Measuring the Complexity of Ultra-Large-Scale Adaptive Systems

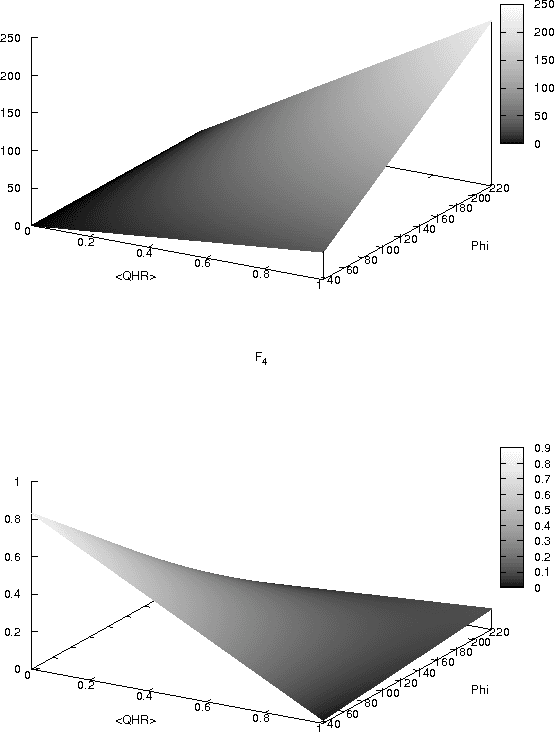
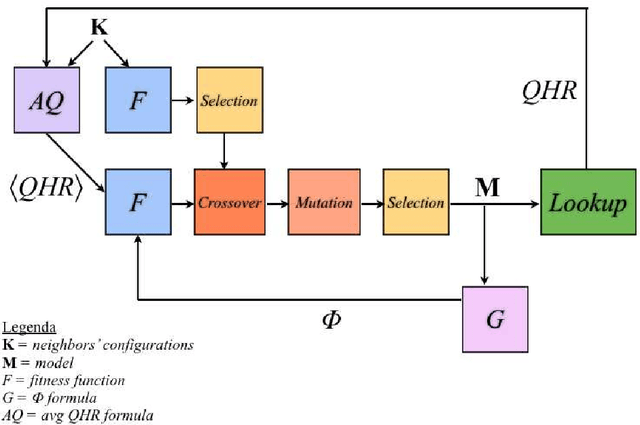
Ultra-large scale (ULS) systems are becoming pervasive. They are inherently complex, which makes their design and control a challenge for traditional methods. Here we propose the design and analysis of ULS systems using measures of complexity, emergence, self-organization, and homeostasis based on information theory. These measures allow the evaluation of ULS systems and thus can be used to guide their design. We evaluate the proposal with a ULS computing system provided with adaptation mechanisms. We show the evolution of the system with stable and also changing workload, using different fitness functions. When the adaptive plan forces the system to converge to a predefined performance level, the nodes may result in highly unstable configurations, that correspond to a high variance in time of the measured complexity. Conversely, if the adaptive plan is less "aggressive", the system may be more stable, but the optimal performance may not be achieved.