Two-Timescale Gradient Descent Ascent Algorithms for Nonconvex Minimax Optimization

We provide a unified analysis of two-timescale gradient descent ascent (TTGDA) for solving structured nonconvex minimax optimization problems in the form of $\min_\textbf{x} \max_{\textbf{y} \in Y} f(\textbf{x}, \textbf{y})$, where the objective function $f(\textbf{x}, \textbf{y})$ is nonconvex in $\textbf{x}$ and concave in $\textbf{y}$, and the constraint set $Y \subseteq \mathbb{R}^n$ is convex and bounded. In the convex-concave setting, the single-timescale GDA achieves strong convergence guarantees and has been used for solving application problems arising from operations research and computer science. However, it can fail to converge in more general settings. Our contribution in this paper is to design the simple deterministic and stochastic TTGDA algorithms that efficiently find one stationary point of the function $\Phi(\cdot) := \max_{\textbf{y} \in Y} f(\cdot, \textbf{y})$. Specifically, we prove the theoretical bounds on the complexity of solving both smooth and nonsmooth nonconvex-concave minimax optimization problems. To our knowledge, this is the first systematic analysis of TTGDA for nonconvex minimax optimization, shedding light on its superior performance in training generative adversarial networks (GANs) and in solving other real-world application problems.

Perseus: A Simple High-Order Regularization Method for Variational Inequalities

This paper settles an open and challenging question pertaining to the design of simple high-order regularization methods for solving smooth and monotone variational inequalities (VIs). A VI involves finding $x^\star \in \mathcal{X}$ such that $\langle F(x), x - x^\star\rangle \geq 0$ for all $x \in \mathcal{X}$ and we consider the setting where $F: \mathbb{R}^d \mapsto \mathbb{R}^d$ is smooth with up to $(p-1)^{th}$-order derivatives. For the case of $p = 2$,~\citet{Nesterov-2006-Constrained} extended the cubic regularized Newton's method to VIs with a global rate of $O(\epsilon^{-1})$. \citet{Monteiro-2012-Iteration} proposed another second-order method which achieved an improved rate of $O(\epsilon^{-2/3}\log(1/\epsilon))$, but this method required a nontrivial binary search procedure as an inner loop. High-order methods based on similar binary search procedures have been further developed and shown to achieve a rate of $O(\epsilon^{-2/(p+1)}\log(1/\epsilon))$. However, such search procedure can be computationally prohibitive in practice and the problem of finding a simple high-order regularization methods remains as an open and challenging question in optimization theory. We propose a $p^{th}$-order method which does \textit{not} require any binary search scheme and is guaranteed to converge to a weak solution with a global rate of $O(\epsilon^{-2/(p+1)})$. A version with restarting attains a global linear and local superlinear convergence rate for smooth and strongly monotone VIs. Further, our method achieves a global rate of $O(\epsilon^{-2/p})$ for solving smooth and non-monotone VIs satisfying the Minty condition; moreover, the restarted version again attains a global linear and local superlinear convergence rate if the strong Minty condition holds.

Near-Optimal Algorithms for Minimax Optimization

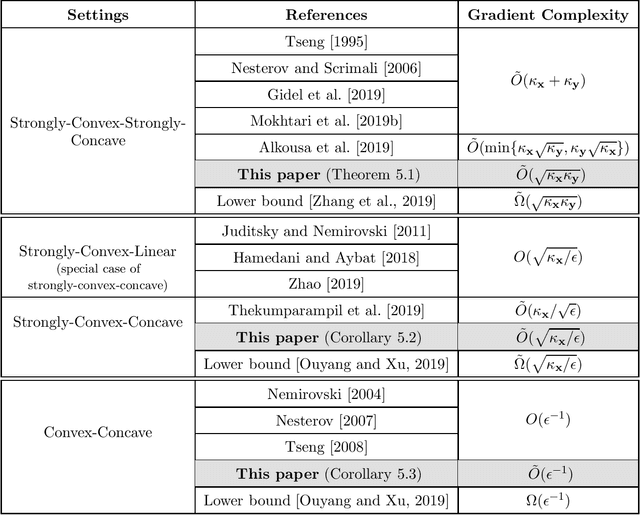
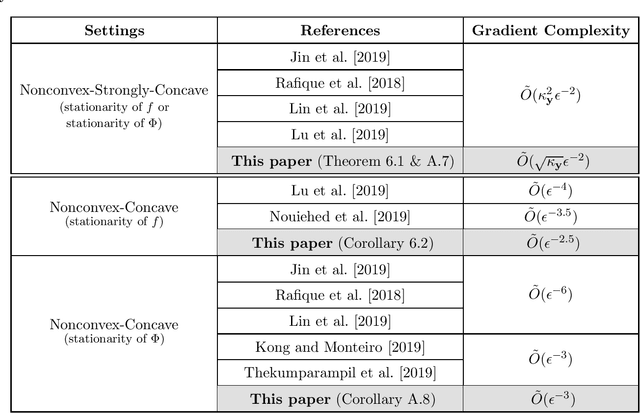
This paper resolves a longstanding open question pertaining to the design of near-optimal first-order algorithms for smooth and strongly-convex-strongly-concave minimax problems. Current state-of-the-art first-order algorithms find an approximate Nash equilibrium using $\tilde{O}(\kappa_{\mathbf x}+\kappa_{\mathbf y})$ or $\tilde{O}(\min\{\kappa_{\mathbf x}\sqrt{\kappa_{\mathbf y}}, \sqrt{\kappa_{\mathbf x}}\kappa_{\mathbf y}\})$ gradient evaluations, where $\kappa_{\mathbf x}$ and $\kappa_{\mathbf y}$ are the condition numbers for the strong-convexity and strong-concavity assumptions. A gap remains between these results and the best existing lower bound $\tilde{\Omega}(\sqrt{\kappa_{\mathbf x}\kappa_{\mathbf y}})$. This paper presents the first algorithm with $\tilde{O}(\sqrt{\kappa_{\mathbf x}\kappa_{\mathbf y}})$ gradient complexity, matching the lower bound up to logarithmic factors. Our new algorithm is designed based on an accelerated proximal point method and an accelerated solver for minimax proximal steps. It can be easily extended to the settings of strongly-convex-concave, convex-concave, nonconvex-strongly-concave, and nonconvex-concave functions. This paper also presents algorithms that match or outperform all existing methods in these settings in terms of gradient complexity, up to logarithmic factors.