Towards a More Complete Theory of Function Preserving Transforms

In this paper, we develop novel techniques that can be used to alter the architecture of a neural network, while maintaining the function it represents. Such operations are known as function preserving transforms and have proven useful in transferring knowledge between networks to evaluate architectures quickly, thus having applications in efficient architectures searches. Our methods allow the integration of residual connections into function preserving transforms, so we call them R2R. We provide a derivation for R2R and show that it yields competitive performance with other function preserving transforms, thereby decreasing the restrictions on deep learning architectures that can be extended through function preserving transforms. We perform a comparative analysis with other function preserving transforms such as Net2Net and Network Morphisms, where we shed light on their differences and individual use cases. Finally, we show the effectiveness of R2R to train models quickly, as well as its ability to learn a more diverse set of filters on image classification tasks compared to Net2Net and Network Morphisms.

Monte Carlo Tree Search with Boltzmann Exploration

Monte-Carlo Tree Search (MCTS) methods, such as Upper Confidence Bound applied to Trees (UCT), are instrumental to automated planning techniques. However, UCT can be slow to explore an optimal action when it initially appears inferior to other actions. Maximum ENtropy Tree-Search (MENTS) incorporates the maximum entropy principle into an MCTS approach, utilising Boltzmann policies to sample actions, naturally encouraging more exploration. In this paper, we highlight a major limitation of MENTS: optimal actions for the maximum entropy objective do not necessarily correspond to optimal actions for the original objective. We introduce two algorithms, Boltzmann Tree Search (BTS) and Decaying ENtropy Tree-Search (DENTS), that address these limitations and preserve the benefits of Boltzmann policies, such as allowing actions to be sampled faster by using the Alias method. Our empirical analysis shows that our algorithms show consistent high performance across several benchmark domains, including the game of Go.

Convex Hull Monte-Carlo Tree Search

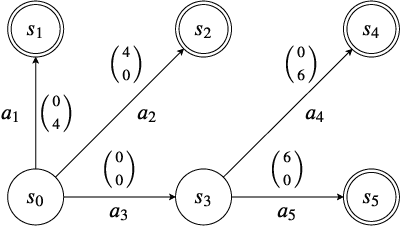
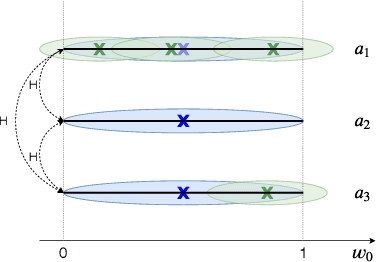
This work investigates Monte-Carlo planning for agents in stochastic environments, with multiple objectives. We propose the Convex Hull Monte-Carlo Tree-Search (CHMCTS) framework, which builds upon Trial Based Heuristic Tree Search and Convex Hull Value Iteration (CHVI), as a solution to multi-objective planning in large environments. Moreover, we consider how to pose the problem of approximating multiobjective planning solutions as a contextual multi-armed bandits problem, giving a principled motivation for how to select actions from the view of contextual regret. This leads us to the use of Contextual Zooming for action selection, yielding Zooming CHMCTS. We evaluate our algorithm using the Generalised Deep Sea Treasure environment, demonstrating that Zooming CHMCTS can achieve a sublinear contextual regret and scales better than CHVI on a given computational budget.