Automated Identification of Vulnerable Devices in Networks using Traffic Data and Deep Learning

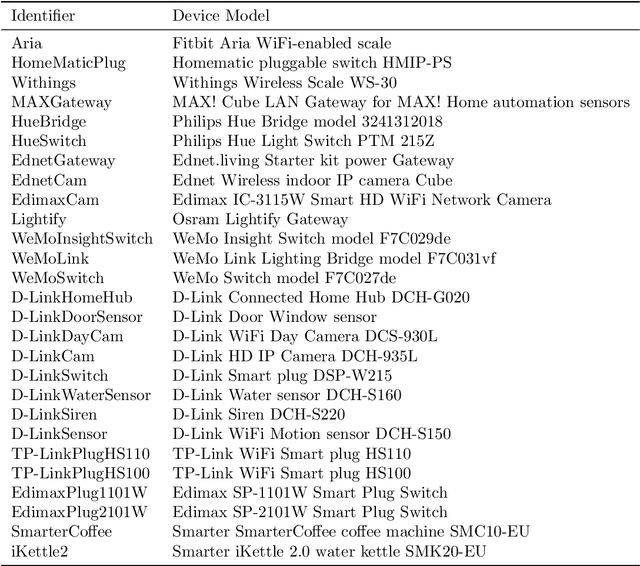
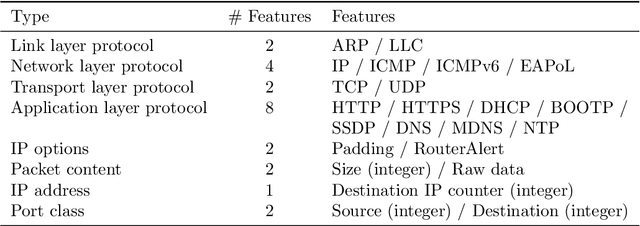
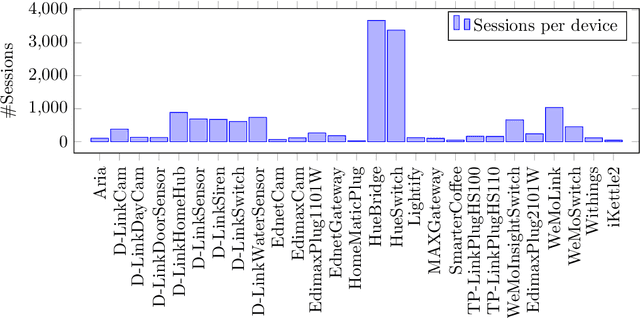
Many IoT devices are vulnerable to attacks due to flawed security designs and lacking mechanisms for firmware updates or patches to eliminate the security vulnerabilities. Device-type identification combined with data from vulnerability databases can pinpoint vulnerable IoT devices in a network and can be used to constrain the communications of vulnerable devices for preventing damage. In this contribution, we present and evaluate two deep learning approaches to the reliable IoT device-type identification, namely a recurrent and a convolutional network architecture. Both deep learning approaches show accuracies of 97% and 98%, respectively, and thereby outperform an up-to-date IoT device-type identification approach using hand-crafted fingerprint features obtaining an accuracy of 82%. The runtime performance for the IoT identification of both deep learning approaches outperforms the hand-crafted approach by three magnitudes. Finally, importance metrics explain the results of both deep learning approaches in terms of the utilization of the analyzed traffic data flow.

On Chase Termination Beyond Stratification

We study the termination problem of the chase algorithm, a central tool in various database problems such as the constraint implication problem, Conjunctive Query optimization, rewriting queries using views, data exchange, and data integration. The basic idea of the chase is, given a database instance and a set of constraints as input, to fix constraint violations in the database instance. It is well-known that, for an arbitrary set of constraints, the chase does not necessarily terminate (in general, it is even undecidable if it does or not). Addressing this issue, we review the limitations of existing sufficient termination conditions for the chase and develop new techniques that allow us to establish weaker sufficient conditions. In particular, we introduce two novel termination conditions called safety and inductive restriction, and use them to define the so-called T-hierarchy of termination conditions. We then study the interrelations of our termination conditions with previous conditions and the complexity of checking our conditions. This analysis leads to an algorithm that checks membership in a level of the T-hierarchy and accounts for the complexity of termination conditions. As another contribution, we study the problem of data-dependent chase termination and present sufficient termination conditions w.r.t. fixed instances. They might guarantee termination although the chase does not terminate in the general case. As an application of our techniques beyond those already mentioned, we transfer our results into the field of query answering over knowledge bases where the chase on the underlying database may not terminate, making existing algorithms applicable to broader classes of constraints.