Topology and morphology design of spherically reconfigurable homogeneous Modular Soft Robots (MSoRos)

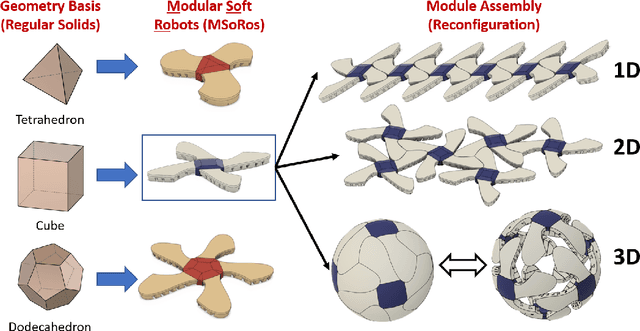
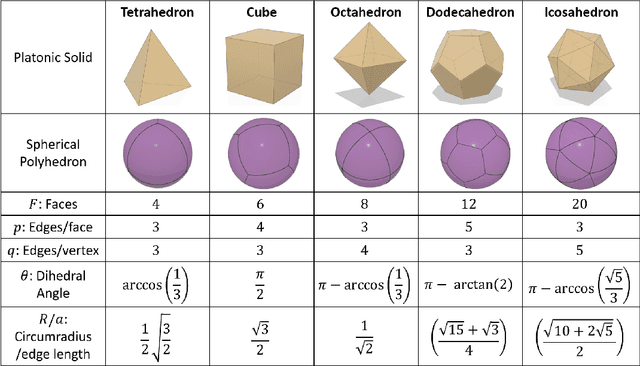
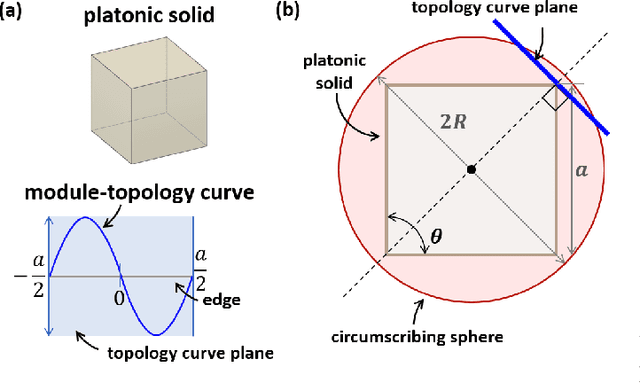
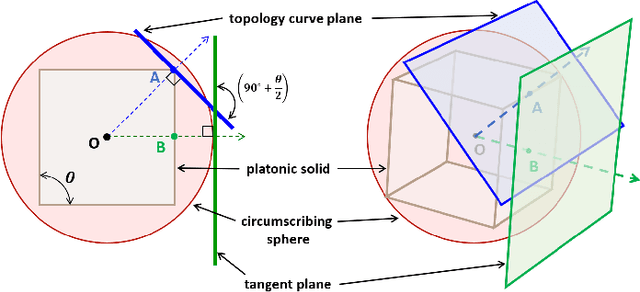
Imagine a swarm of terrestrial robots that can explore an environment, and, upon completion of this task, reconfigure into a spherical ball and roll out. This dimensional change alters the dynamics of locomotion and can assist them to maneuver variable terrains. The sphere-plane reconfiguration is equivalent to projecting a spherical shell onto a plane, an operation which is not possible without distortions. Fortunately, soft materials have potential to adapt to this disparity of the Gaussian curvatures. Modular Soft Robots (MSoRos) have promise of achieving dimensional change by exploiting their continuum and deformable nature. We present topology and morphology design of MSoRos capable of reconfiguring between spherical and planar configurations. Our approach is based in geometry, where a platonic solid determines the number of modules required for plane-to-sphere reconfiguration and the radius of the resulting sphere, e.g., four `tetrahedron-based' or six `cube-based' MSoRos are required for spherical reconfiguration. The methodology involves: (1)inverse orthographic projection of a `module-topology curve' onto the circumscribing sphere to generate the spherical topology,(2)azimuthal projection of the spherical topology onto a tangent plane at the center of the module resulting in the planar topology, and (3)adjusting the limb stiffness and curling ability by manipulating the geometry of cavities to realize a physical finite-width, Motor-Tendon Actuated MSoRo. The topology design is shown to be scale invariant, i.e., scaling of base platonic solid is reflected linearly in spherical and planar topologies. The module-topology curve is optimized for the reconfiguration and locomotion ability using a metric that quantifies sphere-to-plane distortion. The geometry of the cavity optimizes for the limb stiffness and curling ability without compromising the actuator's structural integrity.

Angular Velocity Estimation using Non-coplanar Accelerometer Array

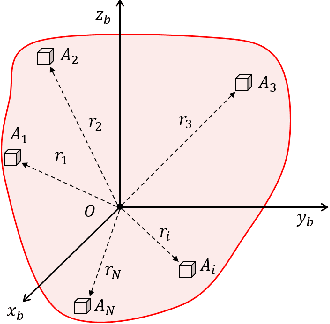
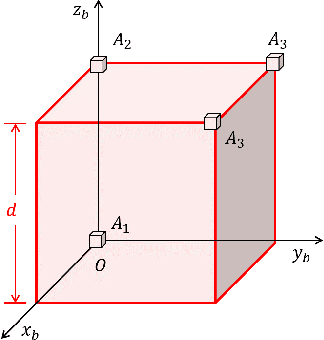
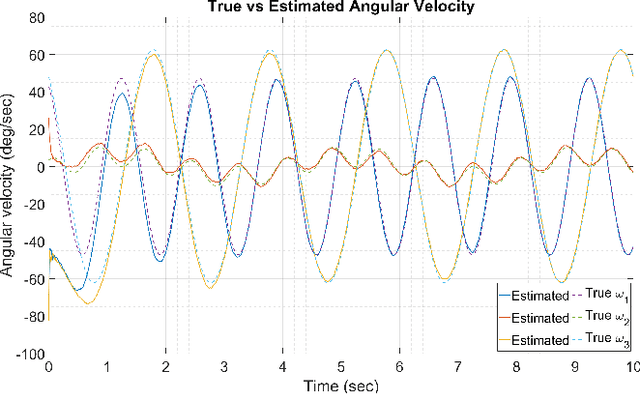
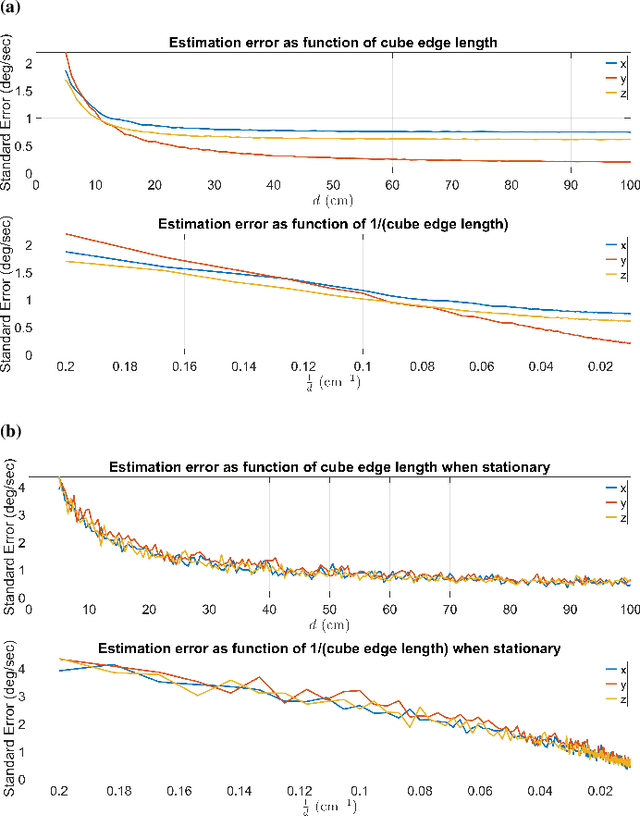
Over the last few decades, Gyro-Free IMUs have been extensively researched to overcome the limitations of gyroscopes. This research presents a Non-coplanar Accelerometer Array (NAA) for estimating angular velocity with non-specific geometric arrangement of four or more triaxial accelerometers with non-coplanarity constraint. The presented proof of non-coplanar spacial arrangement also provides insights into propagation of the sensor noise and construction of the noise covariance matrices. The system noise depends on the singular values of the relative displacement matrix (between the sensors). A dynamical system model with uncorrelated process and measurement noise is proposed where the accelerometer readings are used simultaneously as process and measurement inputs. The angular velocity is estimated using an EKF that discretizes and linearizes the continuous-discrete time dynamical system. The simulations are performed on a Cube-NAA (Cu-NAA) comprising four accelerometers placed at different vertices of a cube. They analyze the estimation error for static and dynamic movement as the distance between the accelerometers is varied. Here, the system noise is observed to decrease inversely with the length of the cube edge as the arrangement is kept identical. Consequently, the simulation results indicate asymptotic decrease in the standard error of estimation with edge length. The experiments are conducted on a Cu-NAA with five reflective optical markers. The reflective markers are visually tracked using VICON to construct the ground truth. This unique experimental setup, apart from providing three degrees of rotational freedom of movement, also allows for three degrees of spacial translation (linear acceleration of the Cu-NAA in space). The simulation and experimental results indicate better performance of the proposed EKF as compared to one with correlated process and measurement noises.