Topology and morphology design of spherically reconfigurable homogeneous Modular Soft Robots (MSoRos)

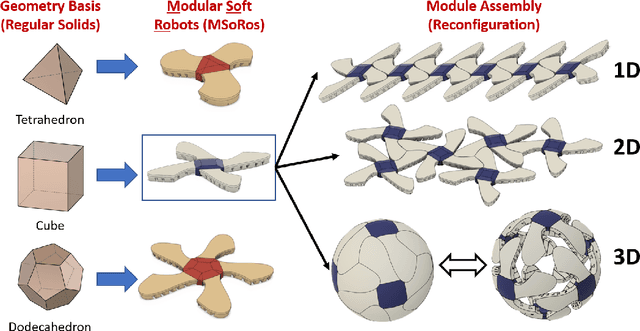
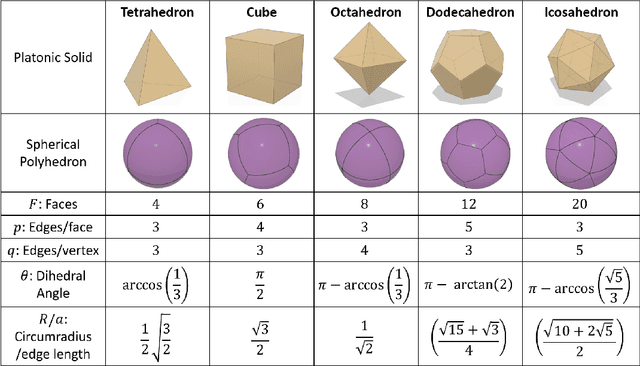
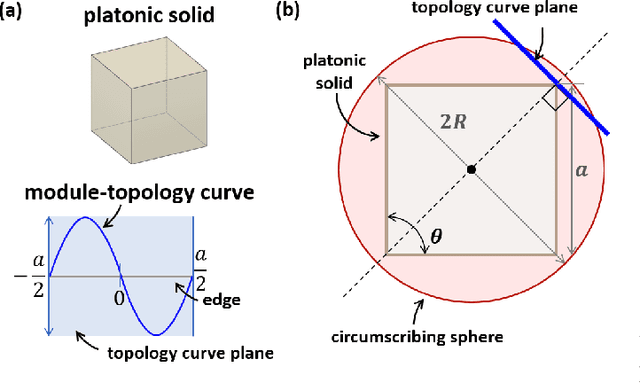
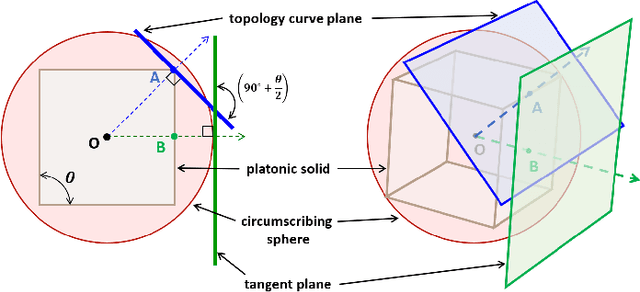
Imagine a swarm of terrestrial robots that can explore an environment, and, upon completion of this task, reconfigure into a spherical ball and roll out. This dimensional change alters the dynamics of locomotion and can assist them to maneuver variable terrains. The sphere-plane reconfiguration is equivalent to projecting a spherical shell onto a plane, an operation which is not possible without distortions. Fortunately, soft materials have potential to adapt to this disparity of the Gaussian curvatures. Modular Soft Robots (MSoRos) have promise of achieving dimensional change by exploiting their continuum and deformable nature. We present topology and morphology design of MSoRos capable of reconfiguring between spherical and planar configurations. Our approach is based in geometry, where a platonic solid determines the number of modules required for plane-to-sphere reconfiguration and the radius of the resulting sphere, e.g., four `tetrahedron-based' or six `cube-based' MSoRos are required for spherical reconfiguration. The methodology involves: (1)inverse orthographic projection of a `module-topology curve' onto the circumscribing sphere to generate the spherical topology,(2)azimuthal projection of the spherical topology onto a tangent plane at the center of the module resulting in the planar topology, and (3)adjusting the limb stiffness and curling ability by manipulating the geometry of cavities to realize a physical finite-width, Motor-Tendon Actuated MSoRo. The topology design is shown to be scale invariant, i.e., scaling of base platonic solid is reflected linearly in spherical and planar topologies. The module-topology curve is optimized for the reconfiguration and locomotion ability using a metric that quantifies sphere-to-plane distortion. The geometry of the cavity optimizes for the limb stiffness and curling ability without compromising the actuator's structural integrity.