Michael B. Giles
Multi Level Monte Carlo methods for a class of ergodic stochastic differential equations
Jul 31, 2016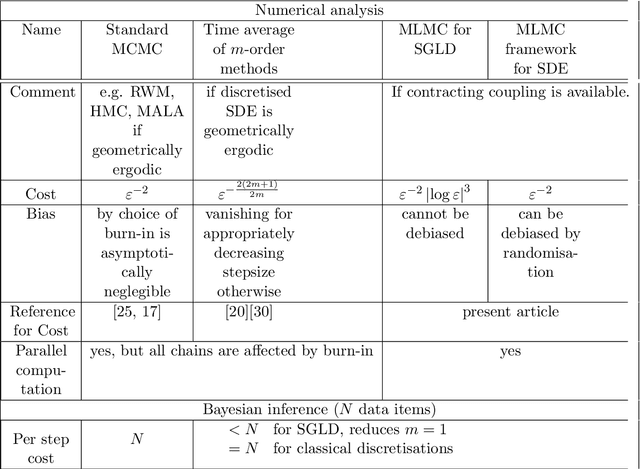



Abstract:We develop a framework that allows the use of the multi-level Monte Carlo (MLMC) methodology (Giles 2015) to calculate expectations with respect to the invariant measures of ergodic SDEs. In that context, we study the (over-damped) Langevin equations with strongly convex potential. We show that, when appropriate contracting couplings for the numerical integrators are available, one can obtain a time-uniform estimates of the MLMC variance in stark contrast to the majority of the results in the MLMC literature. As a consequence, one can approximate expectations with respect to the invariant measure in an unbiased way without the need of a Metropolis- Hastings step. In addition, a root mean square error of $\mathcal{O}(\epsilon)$ is achieved with $\mathcal{O}(\epsilon^{-2})$ complexity on par with Markov Chain Monte Carlo (MCMC) methods, which however can be computationally intensive when applied to large data sets. Finally, we present a multilevel version of the recently introduced Stochastic Gradient Langevin (SGLD) method (Welling and Teh, 2011) built for large datasets applications. We show that this is the first stochastic gradient MCMC method with complexity $\mathcal{O}(\epsilon^{-2}|\log {\epsilon}|^{3})$, which is asymptotically an order $\epsilon$ lower than the $ \mathcal{O}(\epsilon^{-3})$ complexity of all stochastic gradient MCMC methods that are currently available. Numerical experiments confirm our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge