A General Framework for Constrained Bayesian Optimization using Information-based Search

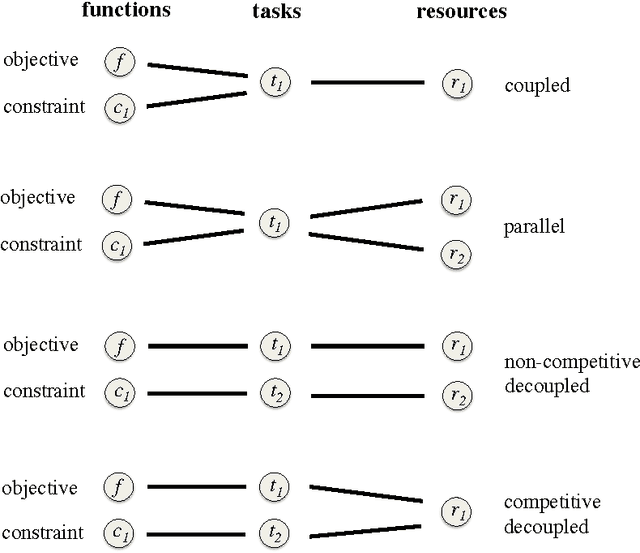
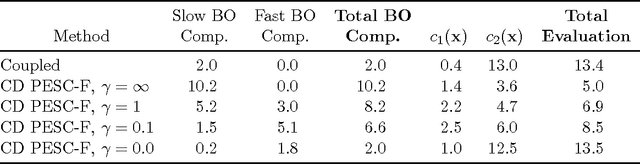
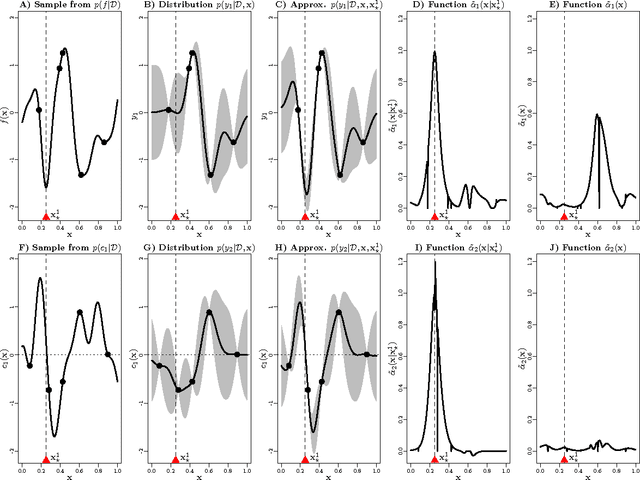
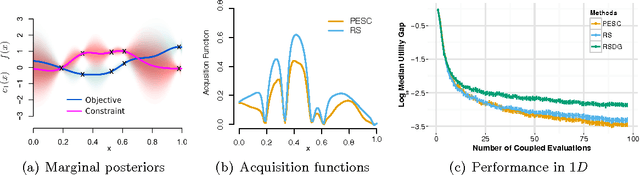
We present an information-theoretic framework for solving global black-box optimization problems that also have black-box constraints. Of particular interest to us is to efficiently solve problems with decoupled constraints, in which subsets of the objective and constraint functions may be evaluated independently. For example, when the objective is evaluated on a CPU and the constraints are evaluated independently on a GPU. These problems require an acquisition function that can be separated into the contributions of the individual function evaluations. We develop one such acquisition function and call it Predictive Entropy Search with Constraints (PESC). PESC is an approximation to the expected information gain criterion and it compares favorably to alternative approaches based on improvement in several synthetic and real-world problems. In addition to this, we consider problems with a mix of functions that are fast and slow to evaluate. These problems require balancing the amount of time spent in the meta-computation of PESC and in the actual evaluation of the target objective. We take a bounded rationality approach and develop partial update for PESC which trades off accuracy against speed. We then propose a method for adaptively switching between the partial and full updates for PESC. This allows us to interpolate between versions of PESC that are efficient in terms of function evaluations and those that are efficient in terms of wall-clock time. Overall, we demonstrate that PESC is an effective algorithm that provides a promising direction towards a unified solution for constrained Bayesian optimization.

Predictive Entropy Search for Bayesian Optimization with Unknown Constraints

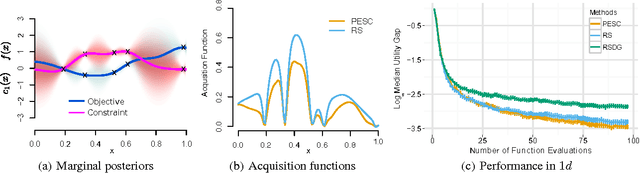
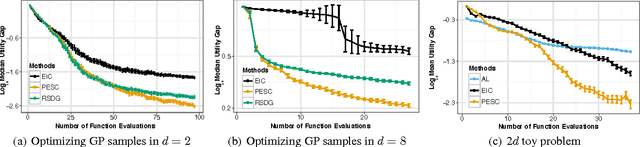
Unknown constraints arise in many types of expensive black-box optimization problems. Several methods have been proposed recently for performing Bayesian optimization with constraints, based on the expected improvement (EI) heuristic. However, EI can lead to pathologies when used with constraints. For example, in the case of decoupled constraints---i.e., when one can independently evaluate the objective or the constraints---EI can encounter a pathology that prevents exploration. Additionally, computing EI requires a current best solution, which may not exist if none of the data collected so far satisfy the constraints. By contrast, information-based approaches do not suffer from these failure modes. In this paper, we present a new information-based method called Predictive Entropy Search with Constraints (PESC). We analyze the performance of PESC and show that it compares favorably to EI-based approaches on synthetic and benchmark problems, as well as several real-world examples. We demonstrate that PESC is an effective algorithm that provides a promising direction towards a unified solution for constrained Bayesian optimization.

Bayesian Optimization with Unknown Constraints

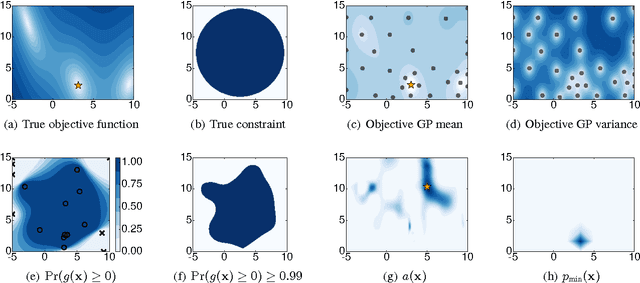
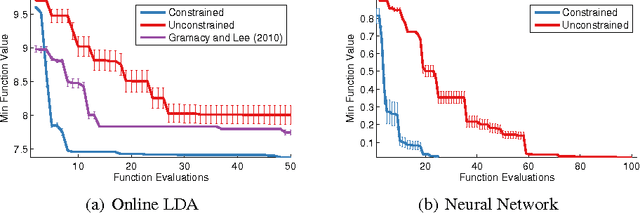
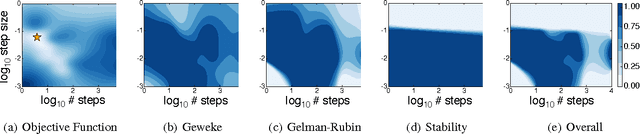
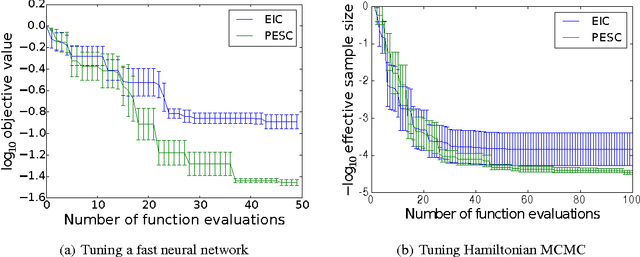
Recent work on Bayesian optimization has shown its effectiveness in global optimization of difficult black-box objective functions. Many real-world optimization problems of interest also have constraints which are unknown a priori. In this paper, we study Bayesian optimization for constrained problems in the general case that noise may be present in the constraint functions, and the objective and constraints may be evaluated independently. We provide motivating practical examples, and present a general framework to solve such problems. We demonstrate the effectiveness of our approach on optimizing the performance of online latent Dirichlet allocation subject to topic sparsity constraints, tuning a neural network given test-time memory constraints, and optimizing Hamiltonian Monte Carlo to achieve maximal effectiveness in a fixed time, subject to passing standard convergence diagnostics.

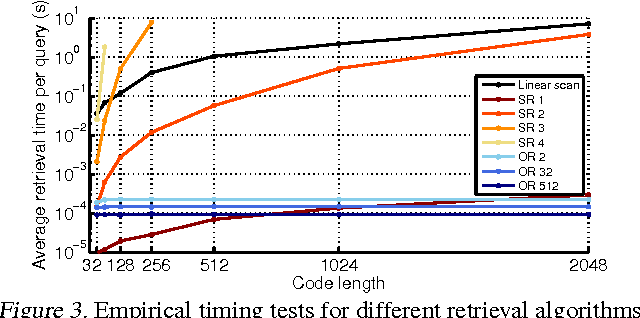
Learning Ordered Representations with Nested Dropout

In this paper, we study ordered representations of data in which different dimensions have different degrees of importance. To learn these representations we introduce nested dropout, a procedure for stochastically removing coherent nested sets of hidden units in a neural network. We first present a sequence of theoretical results in the simple case of a semi-linear autoencoder. We rigorously show that the application of nested dropout enforces identifiability of the units, which leads to an exact equivalence with PCA. We then extend the algorithm to deep models and demonstrate the relevance of ordered representations to a number of applications. Specifically, we use the ordered property of the learned codes to construct hash-based data structures that permit very fast retrieval, achieving retrieval in time logarithmic in the database size and independent of the dimensionality of the representation. This allows codes that are hundreds of times longer than currently feasible for retrieval. We therefore avoid the diminished quality associated with short codes, while still performing retrieval that is competitive in speed with existing methods. We also show that ordered representations are a promising way to learn adaptive compression for efficient online data reconstruction.