Distributed Federated Learning for Vehicular Network Security: Anomaly Detection Benefits and Multi-Domain Attack Threats

In connected and autonomous vehicles, machine learning for safety message classification has become critical for detecting malicious or anomalous behavior. However, conventional approaches that rely on centralized data collection or purely local training face limitations due to the large scale, high mobility, and heterogeneous data distributions inherent in inter-vehicle networks. To overcome these challenges, this paper explores Distributed Federated Learning (DFL), whereby vehicles collaboratively train deep learning models by exchanging model updates among one-hop neighbors and propagating models over multiple hops. Using the Vehicular Reference Misbehavior (VeReMi) Extension Dataset, we show that DFL can significantly improve classification accuracy across all vehicles compared to learning strictly with local data. Notably, vehicles with low individual accuracy see substantial accuracy gains through DFL, illustrating the benefit of knowledge sharing across the network. We further show that local training data size and time-varying network connectivity correlate strongly with the model's overall accuracy. We investigate DFL's resilience and vulnerabilities under attacks in multiple domains, namely wireless jamming and training data poisoning attacks. Our results reveal important insights into the vulnerabilities of DFL when confronted with multi-domain attacks, underlining the need for more robust strategies to secure DFL in vehicular networks.

Compressibility of Network Opinion and Spread States in the Laplacian-Eigenvector Basis

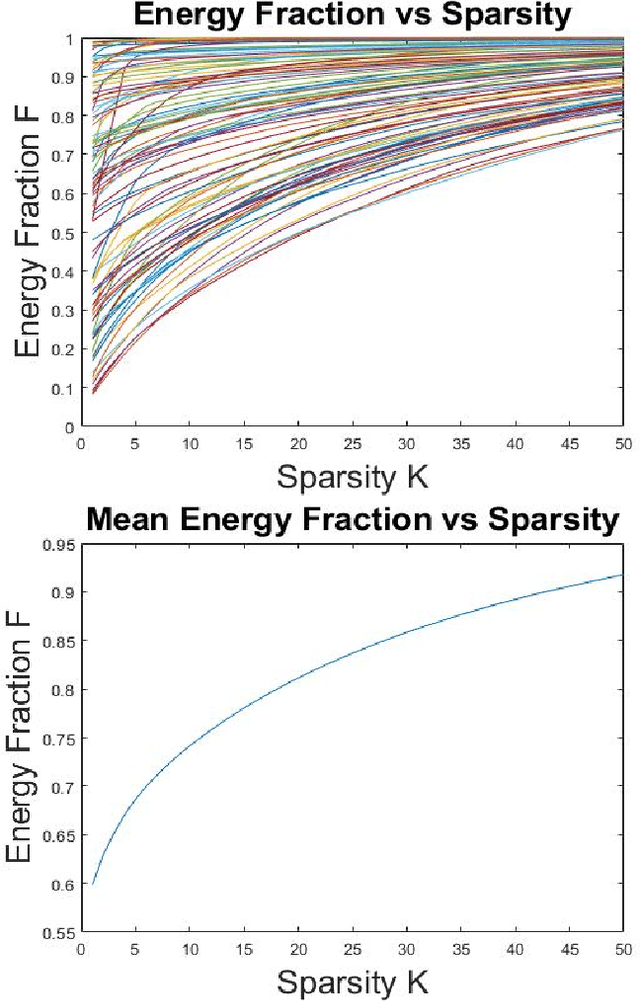
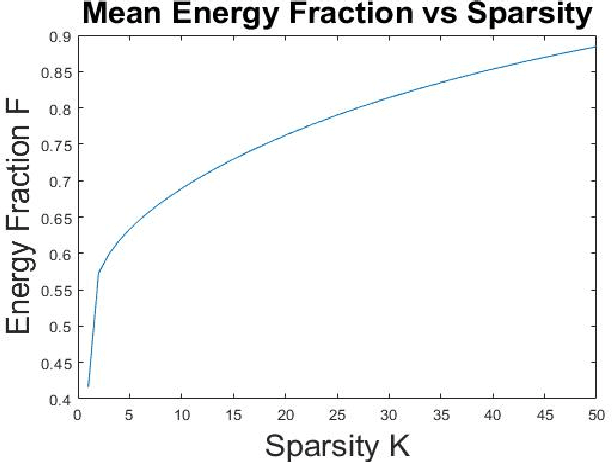
Opinion-evolution and spread processes on networks (e.g., infectious disease spread, opinion formation in social networks) are not only high dimensional but also volatile and multiscale in nature. In this study, we explore whether snapshot data from these processes can admit terse representations. Specifically, using three case studies, we explore whether the data are compressible in the Laplacian-eigenvector basis, in the sense that each snapshot can be approximated well using a (possibly different) small set of basis vectors. The first case study is concerned with a linear consensus model that is subject to a stochastic input at an unknown location; both empirical and formal analyses are used to characterize compressibility. Second, compressibility of state snapshots for a stochastic voter model is assessed via an empirical study. Finally, compressibility is studied for state-level daily COVID-19 positivity-rate data. The three case studies indicate that state snapshots from opinion-evolution and spread processes allow terse representations, which nevertheless capture their rich propagative dynamics.