CD and PMD Effect on Cyclostationarity-Based Timing Recovery for Optical Coherent Receivers

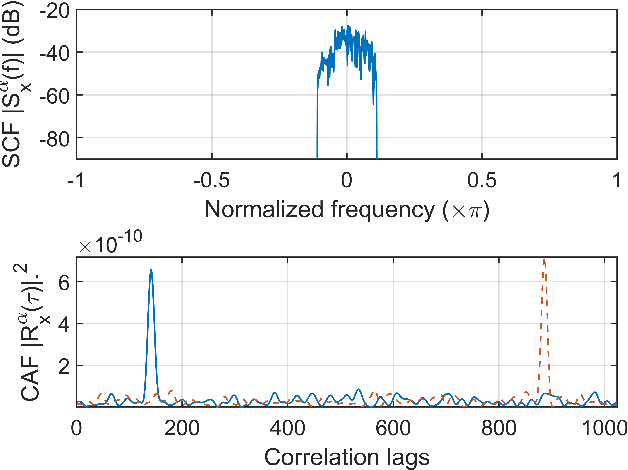
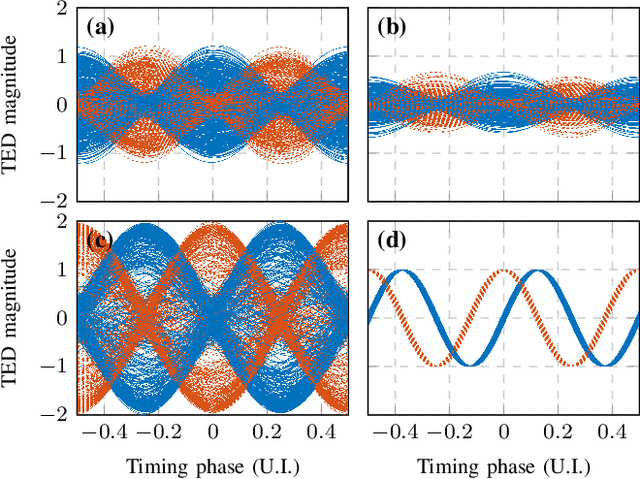
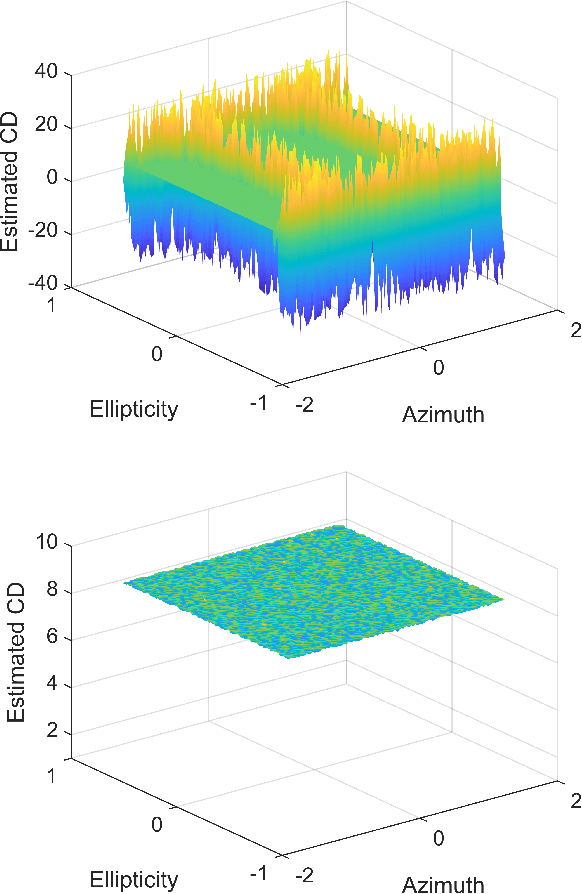
Timing recovery is critical for synchronizing the clocks at the transmitting and receiving ends of a digital coherent communication system. The core of timing recovery is to determine reliably the current sampling error of the local digitizer so that the timing circuit may lock to a stable operation point. Conventional timing phase detectors need to adapt to the optical fiber channel so that the common effects of this channel, such as chromatic dispersion (CD) and polarization mode dispersion (PMD), on the timing phase extraction must be understood. Here we exploit the cyclostationarity of the optical signal and derive a model for studying the CD and PMD effect. We prove that the CD-adjusted cyclic correlation matrix contains full information about timing and PMD, and the determinant of the matrix is a timing phase detector immune to both CD and PMD. We also obtain other results such as a completely PMD-independent CD estimator, etc. Our analysis is supported by both simulations and experiments over a field implemented optical cable.

A Fast Matrix-Completion-Based Approach for Recommendation Systems

Matrix completion is widely used in machine learning, engineering control, image processing, and recommendation systems. Currently, a popular algorithm for matrix completion is Singular Value Threshold (SVT). In this algorithm, the singular value threshold should be set first. However, in a recommendation system, the dimension of the preference matrix keeps changing. Therefore, it is difficult to directly apply SVT. In addition, what the users of a recommendation system need is a sequence of personalized recommended results rather than the estimation of their scores. According to the above ideas, this paper proposes a novel approach named probability completion model~(PCM). By reducing the data dimension, the transitivity of the similar matrix, and singular value decomposition, this approach quickly obtains a completion matrix with the same probability distribution as the original matrix. The approach greatly reduces the computation time based on the accuracy of the sacrifice part, and can quickly obtain a low-rank similarity matrix with data trend approximation properties. The experimental results show that PCM can quickly generate a complementary matrix with similar data trends as the original matrix. The LCS score and efficiency of PCM are both higher than SVT.