CD and PMD Effect on Cyclostationarity-Based Timing Recovery for Optical Coherent Receivers
Paper and Code
Aug 30, 2022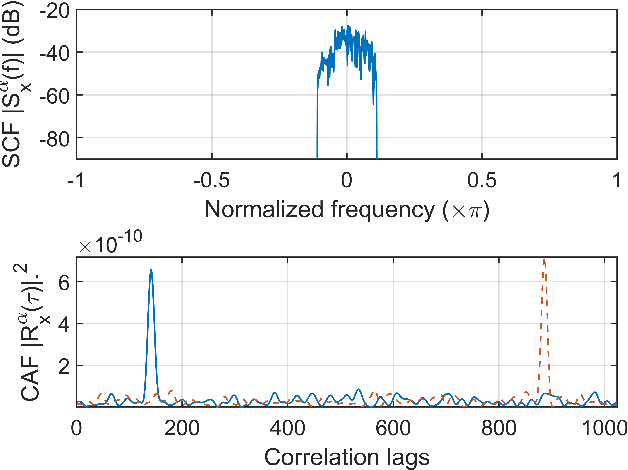

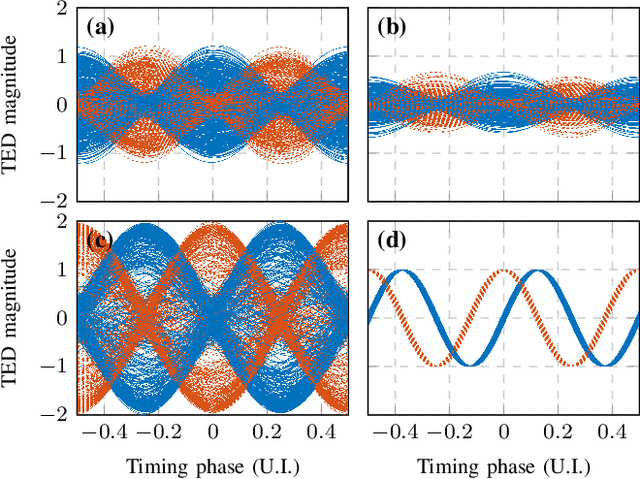
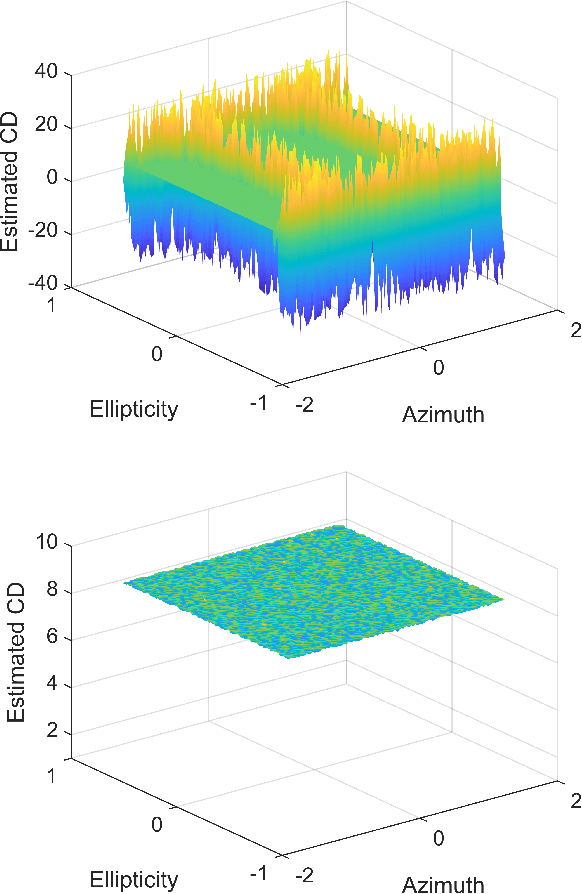
Timing recovery is critical for synchronizing the clocks at the transmitting and receiving ends of a digital coherent communication system. The core of timing recovery is to determine reliably the current sampling error of the local digitizer so that the timing circuit may lock to a stable operation point. Conventional timing phase detectors need to adapt to the optical fiber channel so that the common effects of this channel, such as chromatic dispersion (CD) and polarization mode dispersion (PMD), on the timing phase extraction must be understood. Here we exploit the cyclostationarity of the optical signal and derive a model for studying the CD and PMD effect. We prove that the CD-adjusted cyclic correlation matrix contains full information about timing and PMD, and the determinant of the matrix is a timing phase detector immune to both CD and PMD. We also obtain other results such as a completely PMD-independent CD estimator, etc. Our analysis is supported by both simulations and experiments over a field implemented optical cable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge