Data-Driven Bilateral Generalized Two-Dimensional Quaternion Principal Component Analysis with Application to Color Face Recognition

A new data-driven bilateral generalized two-dimensional quaternion principal component analysis (BiG2DQPCA) is presented to extract the features of matrix samples from both row and column directions. This general framework directly works on the 2D color images without vectorizing and well preserves the spatial and color information, which makes it flexible to fit various real-world applications. A generalized ridge regression model of BiG2DQPCA is firstly proposed with orthogonality constrains on aimed features. Applying the deflation technique and the framework of minorization-maximization, a new quaternion optimization algorithm is proposed to compute the optimal features of BiG2DQPCA and a closed-form solution is obtained at each iteration. A new approach based on BiG2DQPCA is presented for color face recognition and image reconstruction with a new data-driven weighting technique. Sufficient numerical experiments are implemented on practical color face databases and indicate the superiority of BiG2DQPCA over the state-of-the-art methods in terms of recognition accuracies and rates of image reconstruction.

Generalized Two-Dimensional Quaternion Principal Component Analysis with Weighting for Color Image Recognition

A generalized two-dimensional quaternion principal component analysis (G2DQPCA) approach with weighting is presented for color image analysis. As a general framework of 2DQPCA, G2DQPCA is flexible to adapt different constraints or requirements by imposing $L_{p}$ norms both on the constraint function and the objective function. The gradient operator of quaternion vector functions is redefined by the structure-preserving gradient operator of real vector function. Under the framework of minorization-maximization (MM), an iterative algorithm is developed to obtain the optimal closed-form solution of G2DQPCA. The projection vectors generated by the deflating scheme are required to be orthogonal to each other. A weighting matrix is defined to magnify the effect of main features. The weighted projection bases remain the accuracy of face recognition unchanged or moving in a tight range as the number of features increases. The numerical results based on the real face databases validate that the newly proposed method performs better than the state-of-the-art algorithms.

Relaxed 2-D Principal Component Analysis by $L_p$ Norm for Face Recognition

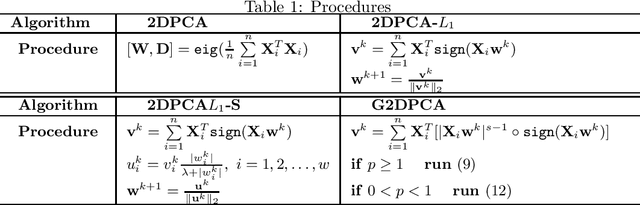
A relaxed two dimensional principal component analysis (R2DPCA) approach is proposed for face recognition. Different to the 2DPCA, 2DPCA-$L_1$ and G2DPCA, the R2DPCA utilizes the label information (if known) of training samples to calculate a relaxation vector and presents a weight to each subset of training data. A new relaxed scatter matrix is defined and the computed projection axes are able to increase the accuracy of face recognition. The optimal $L_p$-norms are selected in a reasonable range. Numerical experiments on practical face databased indicate that the R2DPCA has high generalization ability and can achieve a higher recognition rate than state-of-the-art methods.