Hypergraph Neural Networks Reveal Spatial Domains from Single-cell Transcriptomics Data

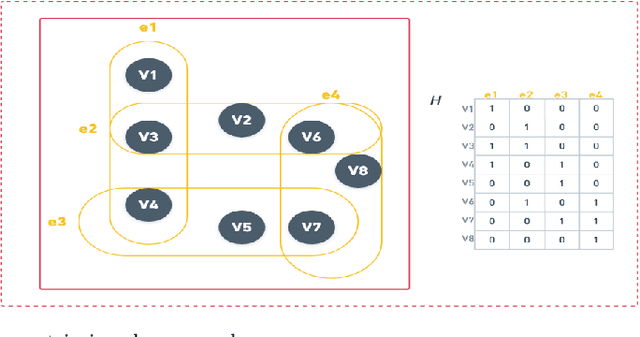
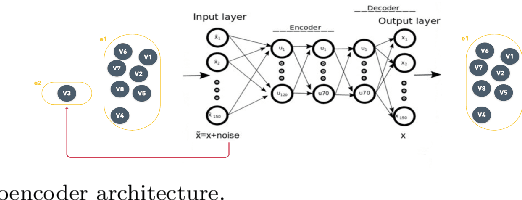
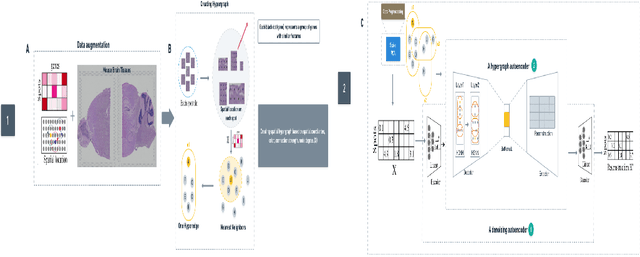
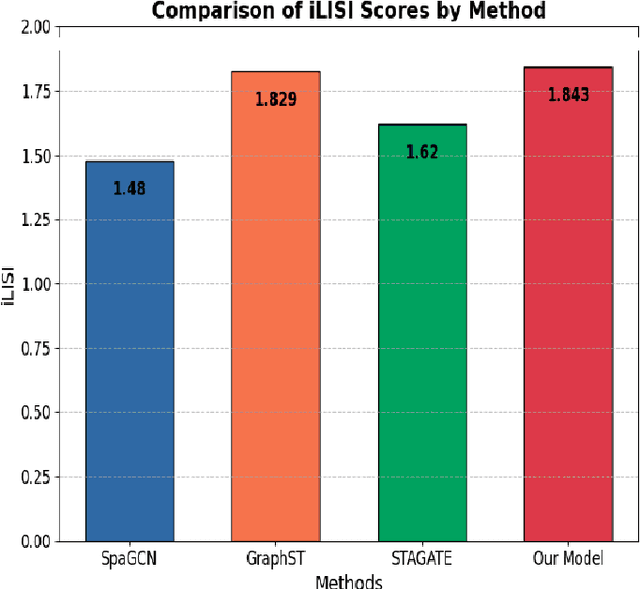
The task of spatial clustering of transcriptomics data is of paramount importance. It enables the classification of tissue samples into diverse subpopulations of cells, which, in turn, facilitates the analysis of the biological functions of clusters, tissue reconstruction, and cell-cell interactions. Many approaches leverage gene expressions, spatial locations, and histological images to detect spatial domains; however, Graph Neural Networks (GNNs) as state of the art models suffer from a limitation in the assumption of pairwise connections between nodes. In the case of domain detection in spatial transcriptomics, some cells are found to be not directly related. Still, they are grouped as the same domain, which shows the incapability of GNNs for capturing implicit connections among the cells. While graph edges connect only two nodes, hyperedges connect an arbitrary number of nodes along their edges, which lets Hypergraph Neural Networks (HGNNs) capture and utilize richer and more complex structural information than traditional GNNs. We use autoencoders to address the limitation of not having the actual labels, which are well-suited for unsupervised learning. Our model has demonstrated exceptional performance, achieving the highest iLISI score of 1.843 compared to other methods. This score indicates the greatest diversity of cell types identified by our method. Furthermore, our model outperforms other methods in downstream clustering, achieving the highest ARI values of 0.51 and Leiden score of 0.60.

Hyperedge Modeling in Hypergraph Neural Networks by using Densest Overlapping Subgraphs

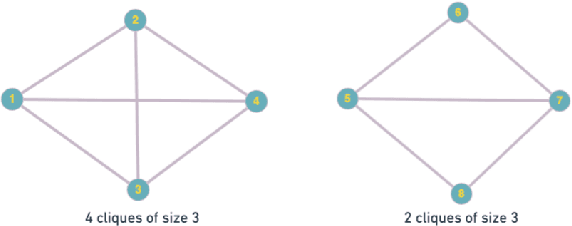
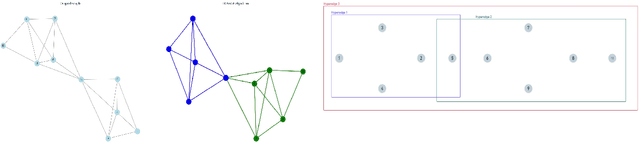
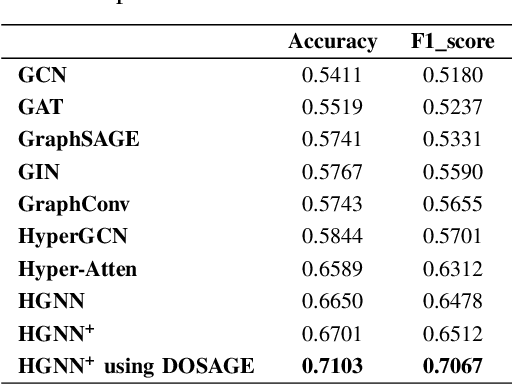
Hypergraphs tackle the limitations of traditional graphs by introducing {\em hyperedges}. While graph edges connect only two nodes, hyperedges connect an arbitrary number of nodes along their edges. Also, the underlying message-passing mechanisms in Hypergraph Neural Networks (HGNNs) are in the form of vertex-hyperedge-vertex, which let HGNNs capture and utilize richer and more complex structural information than traditional Graph Neural Networks (GNNs). More recently, the idea of overlapping subgraphs has emerged. These subgraphs can capture more information about subgroups of vertices without limiting one vertex belonging to just one group, allowing vertices to belong to multiple groups or subgraphs. In addition, one of the most important problems in graph clustering is to find densest overlapping subgraphs (DOS). In this paper, we propose a solution to the DOS problem via Agglomerative Greedy Enumeration (DOSAGE) algorithm as a novel approach to enhance the process of generating the densest overlapping subgraphs and, hence, a robust construction of the hypergraphs. Experiments on standard benchmarks show that the DOSAGE algorithm significantly outperforms the HGNNs and six other methods on the node classification task.