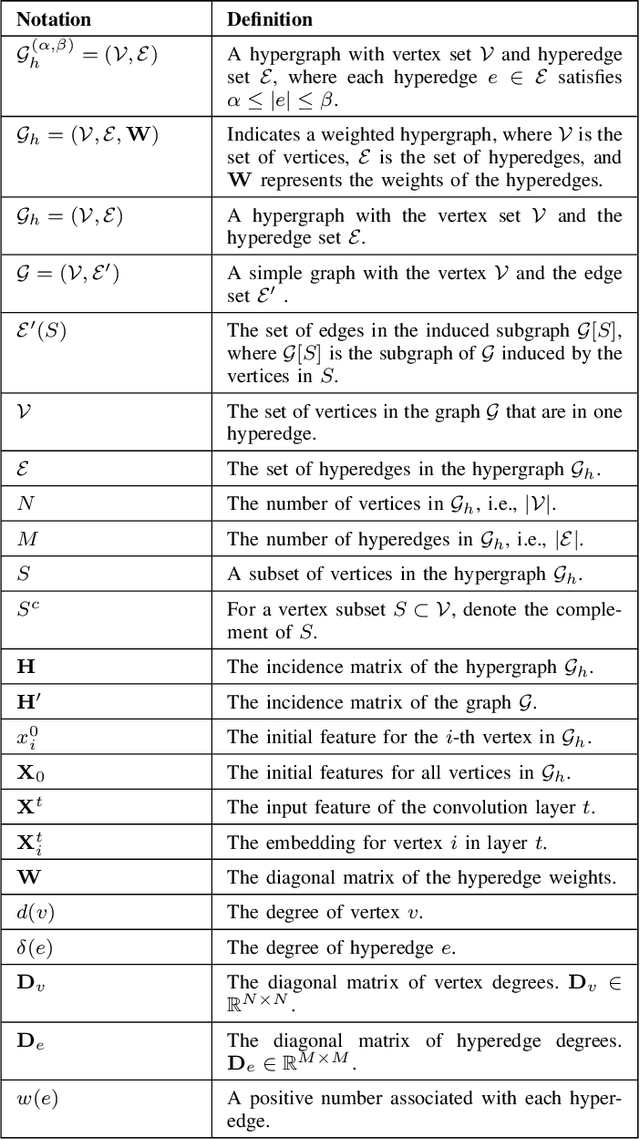
Hyperedge Modeling in Hypergraph Neural Networks by using Densest Overlapping Subgraphs

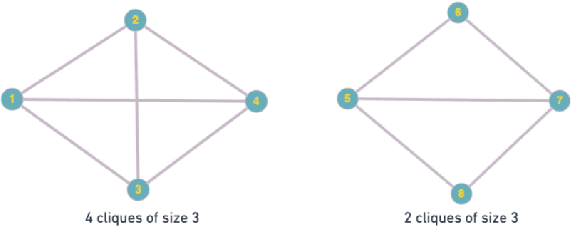
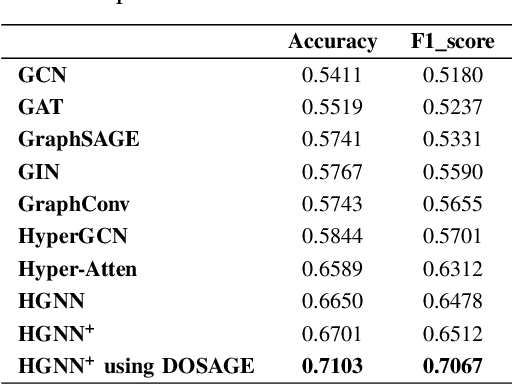
Hypergraphs tackle the limitations of traditional graphs by introducing {\em hyperedges}. While graph edges connect only two nodes, hyperedges connect an arbitrary number of nodes along their edges. Also, the underlying message-passing mechanisms in Hypergraph Neural Networks (HGNNs) are in the form of vertex-hyperedge-vertex, which let HGNNs capture and utilize richer and more complex structural information than traditional Graph Neural Networks (GNNs). More recently, the idea of overlapping subgraphs has emerged. These subgraphs can capture more information about subgroups of vertices without limiting one vertex belonging to just one group, allowing vertices to belong to multiple groups or subgraphs. In addition, one of the most important problems in graph clustering is to find densest overlapping subgraphs (DOS). In this paper, we propose a solution to the DOS problem via Agglomerative Greedy Enumeration (DOSAGE) algorithm as a novel approach to enhance the process of generating the densest overlapping subgraphs and, hence, a robust construction of the hypergraphs. Experiments on standard benchmarks show that the DOSAGE algorithm significantly outperforms the HGNNs and six other methods on the node classification task.