Designing Cellular Manufacturing System in Presence of Alternative Process Plans

In the design of cellular manufacturing systems (CMS), numerous technological and managerial decisions must be made at both the design and operational stages. The first step in designing a CMS involves grouping parts and machines. In this paper, four integer programming formulations are presented for grouping parts and machines in a CMS at both the design and operational levels for a generalized grouping problem, where each part has more than one process plan, and each operation of a process plan can be performed on more than one machine. The minimization of inter-cell and intra-cell movements is achieved by assigning the maximum possible number of consecutive operations of a part type to the same cell and to the same machine, respectively. The suitability of minimizing inter-cell and intra-cell movements as an objective, compared to other objectives such as minimizing investment costs on machines, operating costs, etc., is discussed. Numerical examples are included to illustrate the workings of the formulations.

Solving Generalized Grouping Problems in Cellular Manufacturing Systems Using a Network Flow Model

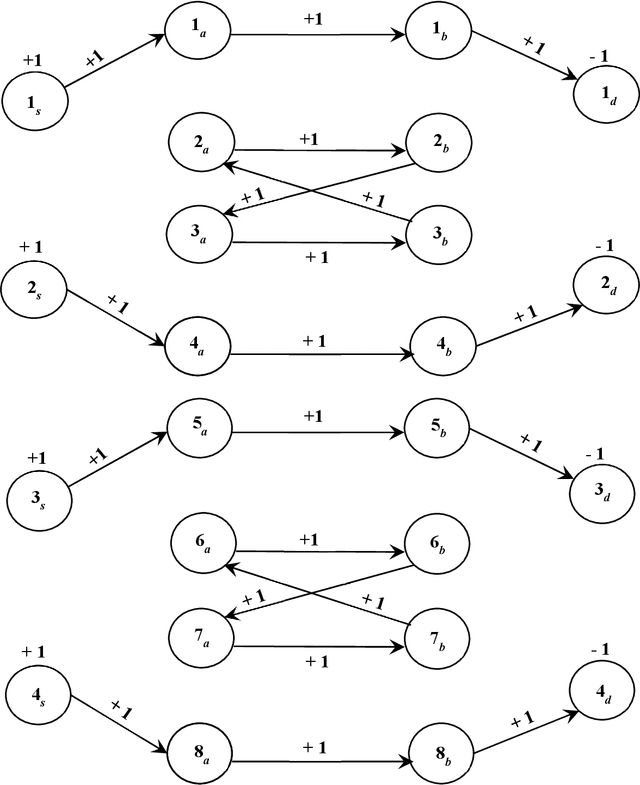
This paper focuses on the generalized grouping problem in the context of cellular manufacturing systems (CMS), where parts may have more than one process route. A process route lists the machines corresponding to each part of the operation. Inspired by the extensive and widespread use of network flow algorithms, this research formulates the process route family formation for generalized grouping as a unit capacity minimum cost network flow model. The objective is to minimize dissimilarity (based on the machines required) among the process routes within a family. The proposed model optimally solves the process route family formation problem without pre-specifying the number of part families to be formed. The process route of family formation is the first stage in a hierarchical procedure. For the second stage (machine cell formation), two procedures, a quadratic assignment programming (QAP) formulation and a heuristic procedure, are proposed. The QAP simultaneously assigns process route families and machines to a pre-specified number of cells in such a way that total machine utilization is maximized. The heuristic procedure for machine cell formation is hierarchical in nature. Computational results for some test problems show that the QAP and the heuristic procedure yield the same results.