Pathological Regularization Regimes in Classification Tasks

In this paper we demonstrate the possibility of a trend reversal in binary classification tasks between the dataset and a classification score obtained from a trained model. This trend reversal occurs for certain choices of the regularization parameter for model training, namely, if the parameter is contained in what we call the pathological regularization regime. For ridge regression, we give necessary and sufficient algebraic conditions on the dataset for the existence of a pathological regularization regime. Moreover, our results provide a data science practitioner with a hands-on tool to avoid hyperparameter choices suffering from trend reversal. We furthermore present numerical results on pathological regularization regimes for logistic regression. Finally, we draw connections to datasets exhibiting Simpson's paradox, providing a natural source of pathological datasets.

Geometry of Polynomial Neural Networks

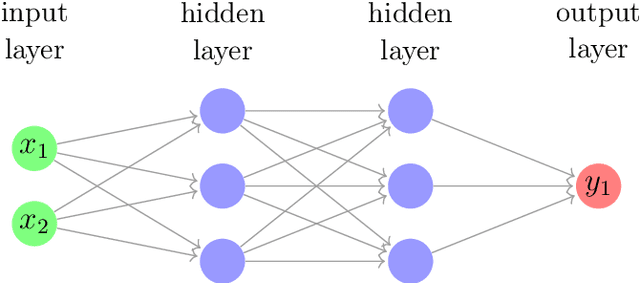
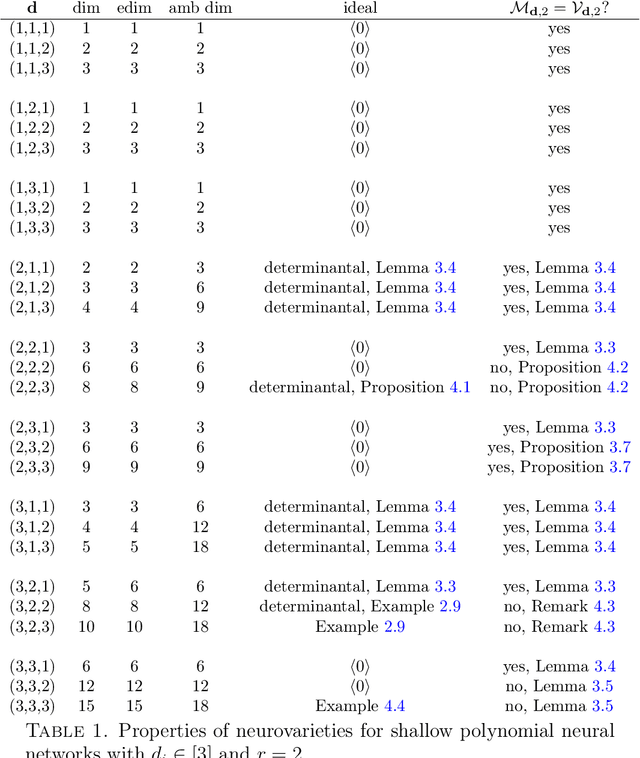
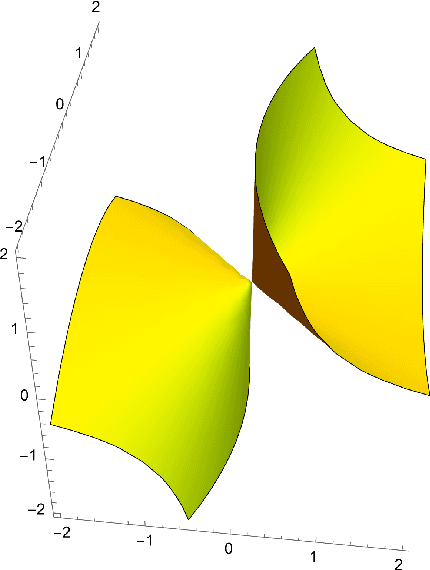
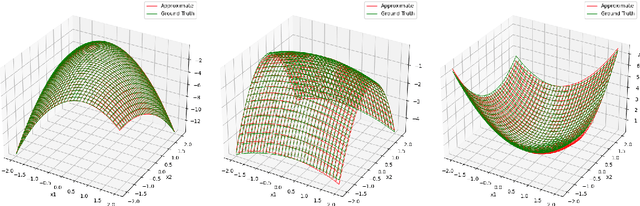
We study the expressivity and learning process for polynomial neural networks (PNNs) with monomial activation functions. The weights of the network parametrize the neuromanifold. In this paper, we study certain neuromanifolds using tools from algebraic geometry: we give explicit descriptions as semialgebraic sets and characterize their Zariski closures, called neurovarieties. We study their dimension and associate an algebraic degree, the learning degree, to the neurovariety. The dimension serves as a geometric measure for the expressivity of the network, the learning degree is a measure for the complexity of training the network and provides upper bounds on the number of learnable functions. These theoretical results are accompanied with experiments.