Self-supervised optimization of random material microstructures in the small-data regime

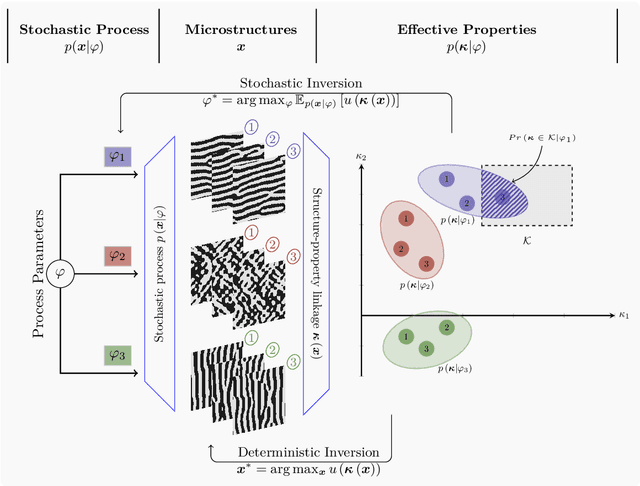
While the forward and backward modeling of the process-structure-property chain has received a lot of attention from the materials community, fewer efforts have taken into consideration uncertainties. Those arise from a multitude of sources and their quantification and integration in the inversion process are essential in meeting the materials design objectives. The first contribution of this paper is a flexible, fully probabilistic formulation of such optimization problems that accounts for the uncertainty in the process-structure and structure-property linkages and enables the identification of optimal, high-dimensional, process parameters. We employ a probabilistic, data-driven surrogate for the structure-property link which expedites computations and enables handling of non-differential objectives. We couple this with a novel active learning strategy, i.e. a self-supervised collection of data, which significantly improves accuracy while requiring small amounts of training data. We demonstrate its efficacy in optimizing the mechanical and thermal properties of two-phase, random media but envision its applicability encompasses a wide variety of microstructure-sensitive design problems.

A probabilistic generative model for semi-supervised training of coarse-grained surrogates and enforcing physical constraints through virtual observables

The data-centric construction of inexpensive surrogates for fine-grained, physical models has been at the forefront of computational physics due to its significant utility in many-query tasks such as uncertainty quantification. Recent efforts have taken advantage of the enabling technologies from the field of machine learning (e.g. deep neural networks) in combination with simulation data. While such strategies have shown promise even in higher-dimensional problems, they generally require large amounts of training data even though the construction of surrogates is by definition a Small Data problem. Rather than employing data-based loss functions, it has been proposed to make use of the governing equations (in the simplest case at collocation points) in order to imbue domain knowledge in the training of the otherwise black-box-like interpolators. The present paper provides a flexible, probabilistic framework that accounts for physical structure and information both in the training objectives as well as in the surrogate model itself. We advocate a probabilistic (Bayesian) model in which equalities that are available from the physics (e.g. residuals, conservation laws) can be introduced as virtual observables and can provide additional information through the likelihood. We further advocate a generative model i.e. one that attempts to learn the joint density of inputs and outputs that is capable of making use of unlabeled data (i.e. only inputs) in a semi-supervised fashion in order to promote the discovery of lower-dimensional embeddings which are nevertheless predictive of the fine-grained model's output.