Self-supervised optimization of random material microstructures in the small-data regime
Paper and Code
Aug 05, 2021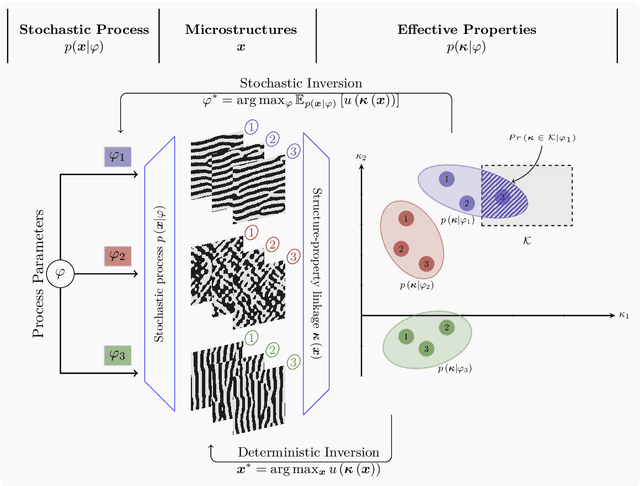
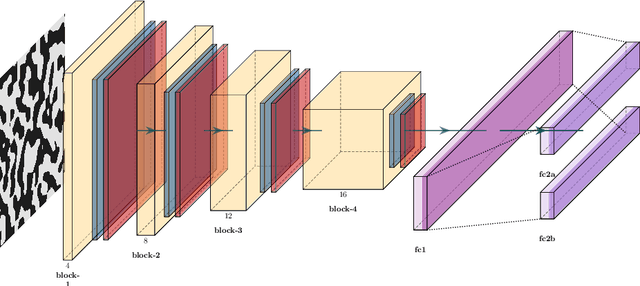


While the forward and backward modeling of the process-structure-property chain has received a lot of attention from the materials community, fewer efforts have taken into consideration uncertainties. Those arise from a multitude of sources and their quantification and integration in the inversion process are essential in meeting the materials design objectives. The first contribution of this paper is a flexible, fully probabilistic formulation of such optimization problems that accounts for the uncertainty in the process-structure and structure-property linkages and enables the identification of optimal, high-dimensional, process parameters. We employ a probabilistic, data-driven surrogate for the structure-property link which expedites computations and enables handling of non-differential objectives. We couple this with a novel active learning strategy, i.e. a self-supervised collection of data, which significantly improves accuracy while requiring small amounts of training data. We demonstrate its efficacy in optimizing the mechanical and thermal properties of two-phase, random media but envision its applicability encompasses a wide variety of microstructure-sensitive design problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge