Mauro Zucchelli
NODDI-SH: a computational efficient NODDI extension for fODF estimation in diffusion MRI
Sep 01, 2017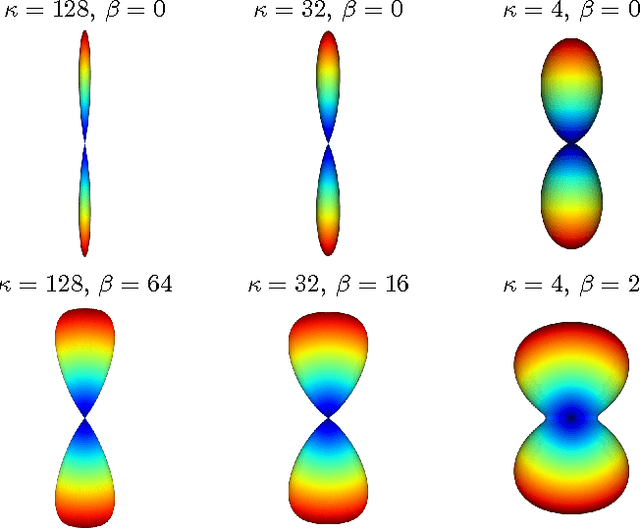
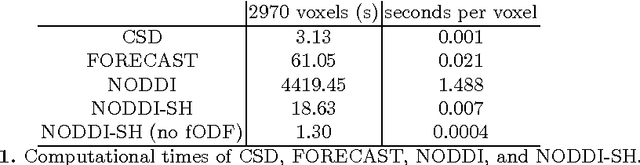
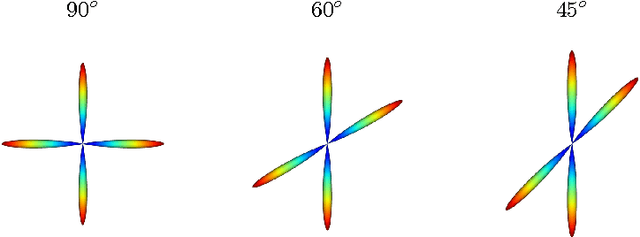
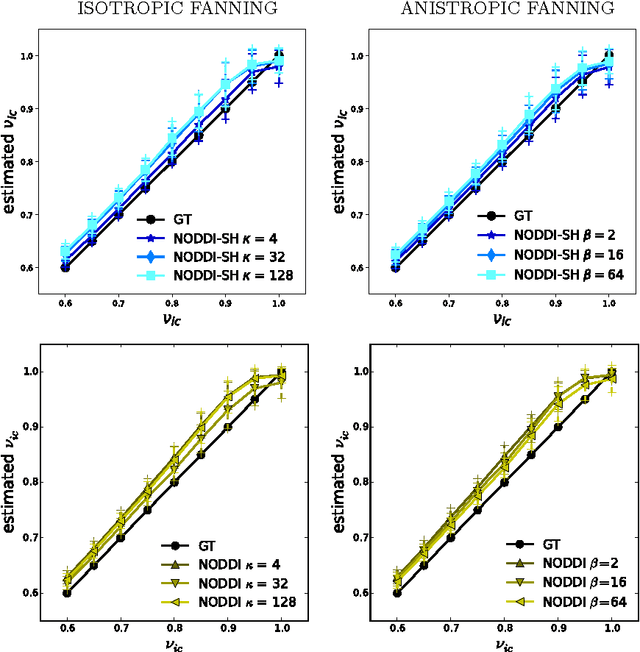
Abstract:Diffusion Magnetic Resonance Imaging (DMRI) is the only non-invasive imaging technique which is able to detect the principal directions of water diffusion as well as neurites density in the human brain. Exploiting the ability of Spherical Harmonics (SH) to model spherical functions, we propose a new reconstruction model for DMRI data which is able to estimate both the fiber Orientation Distribution Function (fODF) and the relative volume fractions of the neurites in each voxel, which is robust to multiple fiber crossings. We consider a Neurite Orientation Dispersion and Density Imaging (NODDI) inspired single fiber diffusion signal to be derived from three compartments: intracellular, extracellular, and cerebrospinal fluid. The model, called NODDI-SH, is derived by convolving the single fiber response with the fODF in each voxel. NODDI-SH embeds the calculation of the fODF and the neurite density in a unified mathematical model providing efficient, robust and accurate results. Results were validated on simulated data and tested on \textit{in-vivo} data of human brain, and compared to and Constrained Spherical Deconvolution (CSD) for benchmarking. Results revealed competitive performance in all respects and inherent adaptivity to local microstructure, while sensibly reducing the computational cost. We also investigated NODDI-SH performance when only a limited number of samples are available for the fitting, demonstrating that 60 samples are enough to obtain reliable results. The fast computational time and the low number of signal samples required, make NODDI-SH feasible for clinical application.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge