Learning Brave Assumption-Based Argumentation Frameworks via ASP

Assumption-based Argumentation (ABA) is advocated as a unifying formalism for various forms of non-monotonic reasoning, including logic programming. It allows capturing defeasible knowledge, subject to argumentative debate. While, in much existing work, ABA frameworks are given up-front, in this paper we focus on the problem of automating their learning from background knowledge and positive/negative examples. Unlike prior work, we newly frame the problem in terms of brave reasoning under stable extensions for ABA. We present a novel algorithm based on transformation rules (such as Rote Learning, Folding, Assumption Introduction and Fact Subsumption) and an implementation thereof that makes use of Answer Set Programming. Finally, we compare our technique to state-of-the-art ILP systems that learn defeasible knowledge.

ABA Learning via ASP

Recently, ABA Learning has been proposed as a form of symbolic machine learning for drawing Assumption-Based Argumentation frameworks from background knowledge and positive and negative examples. We propose a novel method for implementing ABA Learning using Answer Set Programming as a way to help guide Rote Learning and generalisation in ABA Learning.

Learning Assumption-based Argumentation Frameworks

We propose a novel approach to logic-based learning which generates assumption-based argumentation (ABA) frameworks from positive and negative examples, using a given background knowledge. These ABA frameworks can be mapped onto logic programs with negation as failure that may be non-stratified. Whereas existing argumentation-based methods learn exceptions to general rules by interpreting the exceptions as rebuttal attacks, our approach interprets them as undercutting attacks. Our learning technique is based on the use of transformation rules, including some adapted from logic program transformation rules (notably folding) as well as others, such as rote learning and assumption introduction. We present a general strategy that applies the transformation rules in a suitable order to learn stratified frameworks, and we also propose a variant that handles the non-stratified case. We illustrate the benefits of our approach with a number of examples, which show that, on one hand, we are able to easily reconstruct other logic-based learning approaches and, on the other hand, we can work out in a very simple and natural way problems that seem to be hard for existing techniques.

Ontology-based Representation and Reasoning on Process Models: A Logic Programming Approach

We propose a framework grounded in Logic Programming for representing and reasoning about business processes from both the procedural and ontological point of views. In particular, our goal is threefold: (1) define a logical language and a formal semantics for process models enriched with ontology-based annotations; (2) provide an effective inference mechanism that supports the combination of reasoning services dealing with the structural definition of a process model, its behavior, and the domain knowledge related to the participating business entities; (3) implement such a theoretical framework into a process modeling and reasoning platform. To this end we define a process ontology coping with a relevant fragment of the popular BPMN modeling notation. The behavioral semantics of a process is defined as a state transition system by following an approach similar to the Fluent Calculus, and allows us to specify state change in terms of preconditions and effects of the enactment of activities. Then we show how the procedural process knowledge can be seamlessly integrated with the domain knowledge specified by using the OWL 2 RL rule-based ontology language. Our framework provides a wide range of reasoning services, including CTL model checking, which can be performed by using standard Logic Programming inference engines through a goal-oriented, efficient, sound and complete evaluation procedure. We also present a software environment implementing the proposed framework, and we report on an experimental evaluation of the system, whose results are encouraging and show the viability of the approach.

Generalization Strategies for the Verification of Infinite State Systems

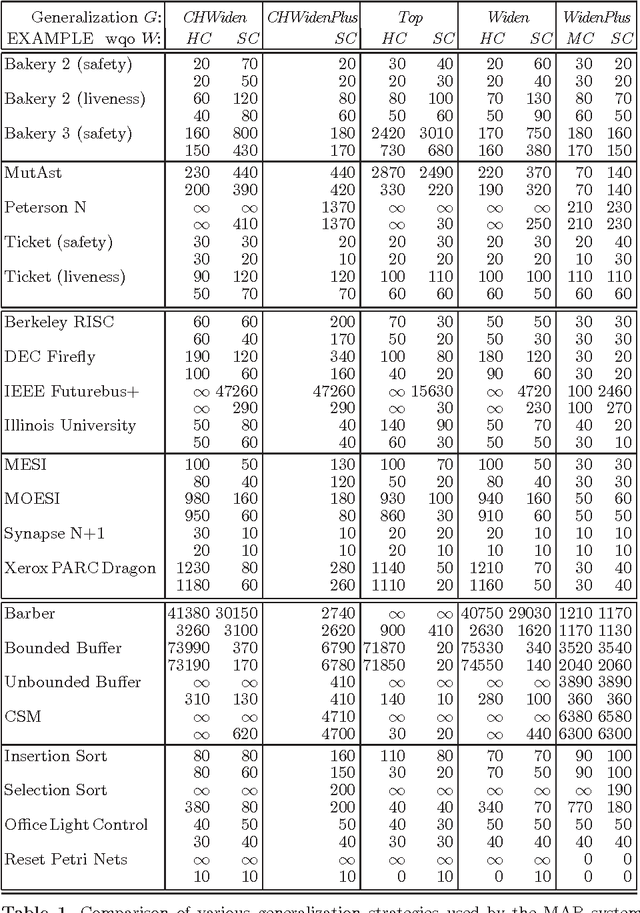
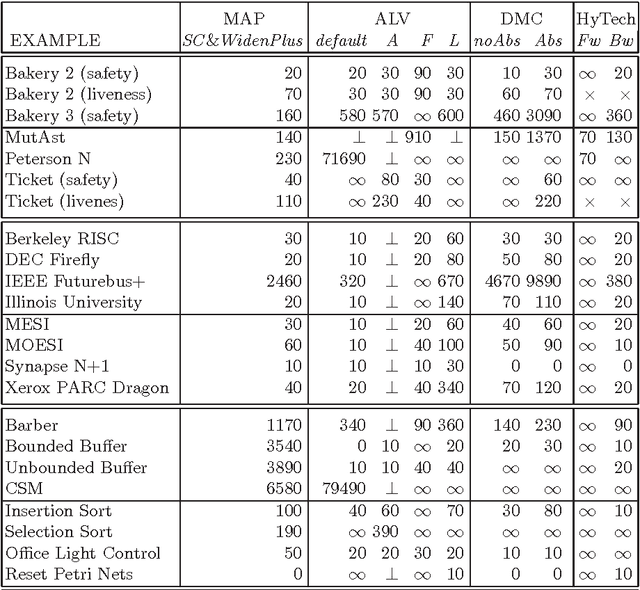
We present a method for the automated verification of temporal properties of infinite state systems. Our verification method is based on the specialization of constraint logic programs (CLP) and works in two phases: (1) in the first phase, a CLP specification of an infinite state system is specialized with respect to the initial state of the system and the temporal property to be verified, and (2) in the second phase, the specialized program is evaluated by using a bottom-up strategy. The effectiveness of the method strongly depends on the generalization strategy which is applied during the program specialization phase. We consider several generalization strategies obtained by combining techniques already known in the field of program analysis and program transformation, and we also introduce some new strategies. Then, through many verification experiments, we evaluate the effectiveness of the generalization strategies we have considered. Finally, we compare the implementation of our specialization-based verification method to other constraint-based model checking tools. The experimental results show that our method is competitive with the methods used by those other tools. To appear in Theory and Practice of Logic Programming (TPLP).