Causal Structure Learning: a Bayesian approach based on random graphs

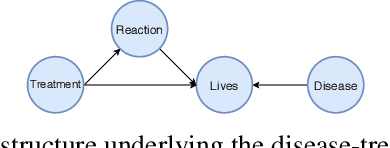
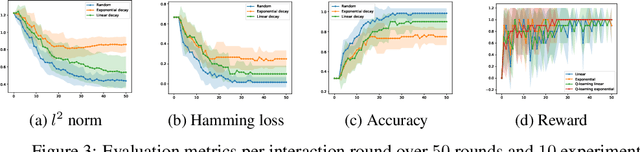
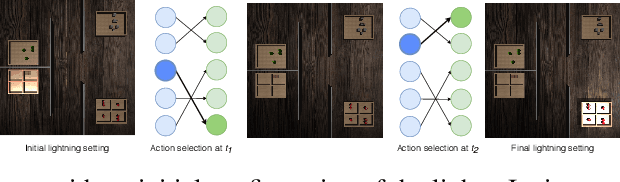
A Random Graph is a random object which take its values in the space of graphs. We take advantage of the expressibility of graphs in order to model the uncertainty about the existence of causal relationships within a given set of variables. We adopt a Bayesian point of view in order to capture a causal structure via interaction and learning with a causal environment. We test our method over two different scenarios, and the experiments mainly confirm that our technique can learn a causal structure. Furthermore, the experiments and results presented for the first test scenario demonstrate the usefulness of our method to learn a causal structure as well as the optimal action. On the other hand the second experiment, shows that our proposal manages to learn the underlying causal structure of several tasks with different sizes and different causal structures.

Reinforcement Learning is not a Causal problem

We use an analogy between non-isomorphic mathematical structures defined over the same set and the algebras induced by associative and causal levels of information in order to argue that Reinforcement Learning, in its current formulation, is not a causal problem, independently if the motivation behind it has to do with an agent taking actions.

von Neumann-Morgenstern and Savage Theorems for Causal Decision Making

Decision making under uncertain conditions has been well studied when uncertainty can only be considered at the associative level of information. The classical Theorems of von Neumann-Morgenstern and Savage provide a formal criterion for rationally making choices using associative information. We provide here a previous result from Pearl and show that it can be considered as a causal version of the von Neumann-Morgenstern Theorem; furthermore, we consider the case when the true causal mechanism that controls the environment is unknown to the decision maker and propose a causal version of the Savage Theorem. As applications, we argue how previous optimal action learning methods for causal environments fit within the Causal Savage Theorem we present thus showing the utility of our result in the justification and design of learning algorithms; furthermore, we define a Causal Nash Equilibria for a strategic game in a causal environment in terms of the preferences induced by our Causal Decision Making Theorem.